УРОК 60
Тема. Решение логарифмических неравенств
Цель урока. Формирование умений учащихся решать логарифмические неравенства.
И. Проверка домашнего задания
1. Два ученика воспроизводят решение упражнений№ 55 (2), 56 (3).
2. Коллективное решение упражнений № 57 (1; 3).
II. Анализ самостоятельной работы, проведенной на предыдущем уроке
III. Восприятие и осознание решения простейших логарифмических неравенств
Как известно, логарифмическая функция у = logа х возрастает при a > 1 и убывает при 0 a 1. Из возрастания функции у = logа x в первом случае и убывание - во втором случае следует:
1) При a > 1 неравенство logа х2 > logа х1 равносильна системе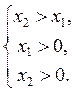 
2) При 0 a 1 неравенство logа х2 > logа х1 равносильна системе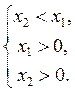 
Рассмотрим примеры.
Пример 1. Решите неравенство log2 x 3.
Решение
Поскольку 3 = log223 = log28, то запишем данное неравенство в виде log2 x log28. Поскольку функция
у = log2x возрастающая при х > 0, то имеем: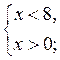 
следовательно, 0 х 8 (рис. 166).
Ответ: х 
(0; 8).
Пример 2. Решите неравенство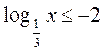 
.
Решение
Запишем данное неравенство в виде:
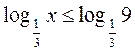. Поскольку функция у = 
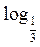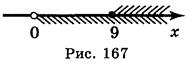
х убывающая при х > 0, имеем: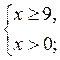 
следовательно, х 
9 (рис. 167).
Ответ: х 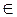[9; + 
).
Как правило, логарифмическое неравенство сводится к неравенств вида: logaf(x) > logag(x), где а > 0, а ≠ 1.
Если а > 1, то неравенство logaf(x) > logag(x) равносильно системе неравенств: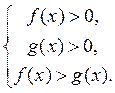 
Если 0 а 1, то неравенство logaf(x) > logag(x) равносильно системе неравенств: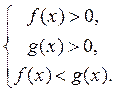 
Пример 3. Решите неравенство: loggg(x2 + x) > -1.
Решение
Так как - 1 = log0,50,5-1 = log0,52, то log0,5(x2 + х) > log0,52.
Полученное неравенство равносильно системе
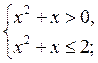
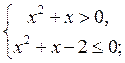
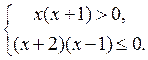
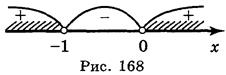
Решением первого неравенства (рис. 168) является (-; -1)
(0; +).
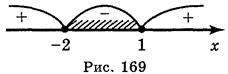
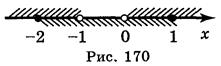
Решением второго неравенства (рис. 169) [-2; 1].
Тогда имеем (рис. 170) x [-2;-1)(0;1].
Ответ: [-2; -1)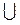(0; 1].
IV. формирование умений решать логарифмические неравенства
Выполнение упражнений№ 58 (2; 3; 7; 8; 10; 11; 12).
V. Подведение итогов урока
VI. Домашнее задание
Раздел V § 3. Вопросы и задания для повторения раздела V № 33-34. Упражнение№ 58 (1; 4; 5; 6; 9).