УРОК 60

Тема. Прямоугольный параллелепипед и его объем

Цель: сформировать понятие о прямоугольный параллелепипед, куб, линейные измерения прямоугольного параллелепипеда, единицы измерения объема; научить учащихся распознавать прямоугольный параллелепипед, куб, называть их элементы, единицы измерения объема, записывать формулы объема прямоугольного параллелепипеда и куба; решать простейшие задачи на применение этих формул.

Тип урока: усвоение новых знаний.

Оборудование: набор игральных кубиков, демонстрационная модель прямоугольного параллелепипеда и куба.

Ход урока

I. Актуализация опорных знаний

Устные упражнения

1. Найдите периметр прямоугольника, площадь которого равен 28 см², а одна из его сторон 7 см.

2. На рис. 85 изображены геометрические фигуры.

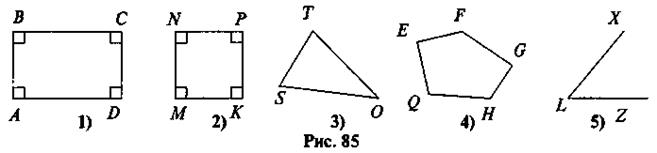
Назовите эти фигуры. Как их обозначить? Назовите вершины и стороны этих фигур. Какая фигура «лишняя»?

3. Заполните величины, пропущенные в цепочках:

4. Петрик Тяпляпкін начертил квадрат и нашел его периметр и площадь. Выяснилось: Р = 20 см, S = 36 см². Правильно ли он подсчитал?

II. Усвоение новых знаний

@ Элемент наглядности является очень важным во время ознакомления учащихся с геометрическим материалом в любом классе, а особенно для пятиклассников, поэтому работу на этом уроке надо организовать так, чтобы все объяснения учителя сопровождались, если это возможно, демонстрациями.

Итак, начать объяснения лучше с того, что показать ученикам, как из кубиков складываются геометрические тела разной формы (можно взять за пример тела, изображенные на рис. 141 п. 21 учебника).

Знакомя учащихся с понятием «прямоугольный параллелепипед», надо показать как можно больше предметов окружающей среды, имеющих форму прямоугольного параллелепипеда, и предложить учащимся привести свои примеры таких предметов.

Во время ознакомление учащихся с понятиями «грань», «ребро», «вершина» прямоугольного параллелепипеда лучше сначала показать эти элементы на демонстрационной модели, а потом уже переходить к рисунку в учебнике, работа с рисунком вызывает в некоторых учащихся затруднения.

Также желательно объяснить ученикам, что прямоугольный параллелепипед - это тело, которое состоит из известных им геометрических фигур - отрезков (ребра) и прямоугольников (грани). А поэтому эти геометрические фигуры можно измерить и тогда получить такие величины:

1) длина всех ребер прямоугольного параллелепипеда равна

4(a + b + c) = 4a + 4b + 4c (если а, b, с - измерения прямоугольного параллелепипеда);

2) площадь поверхности прямоугольного параллелепипеда равна

(ab + bc + ac) = 2ab + 2bc + 2ac.

После ознакомления с элементами прямоугольного параллелепипеда и их свойствами учащиеся выполняют устные задачи.

Задача 1. На рисунке (рис. 86) изображен прямоугольный параллелепипед ABCDKMNP. Назовите:

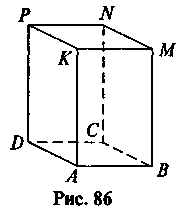
1) нижнюю грань, верхнюю грань;

2) боковые ребра;

3) ребра, равные ребру АВ;

4) вершины, которые принадлежат заданной грани;

5) грань, которая равна грани BMNC.

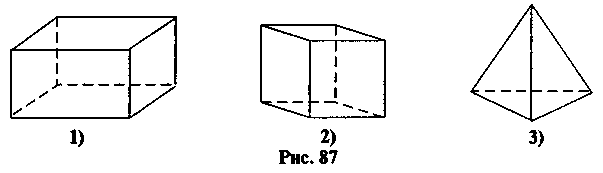
Задание 2. Которые фигуры на рис. 87 лишние? Почему?

Задача 3. Степа Смєкалкін решил сделать модель прямоугольного параллелепипеда из проволоки. Или хватит ли ему для этого 1 м провода, если замеры модели равны 5 см, 10 см, 15 cm?

Задача 4. Степа Смєкалкін решил сделать бумажную модель прямоугольного параллелепипеда с измерениями 3 см, 4 см и 5 см. Хватит ли ему для этого листа картона площадью 1 дм²?

@ После выполнения этого задания учитель показывает модель куба, учащиеся знакомятся с понятием куба (прямоугольного параллелепипеда, у которого все измерения равны) и его свойствами (каждая грань куба - квадрат, следовательно, площадь поверхности куба вычисляется по формуле S = 6a², где а² - площадь одной грани куба).

После этого ученикам может быть предложено такое задание.

Задание 5. Одного раз на уроке учитель предложил Пете Тяпляпкіну найти площадь поверхности куба, который он держал в руках.

- Это очень просто, - бодро начал Петрик. - Сначала измерим два ребра, выходят из одной вершины. Первое равна 10 см, вторая 10 см, следовательно, площадь этого грани 10 · 10 = 100 см². Теперь измерим другие два ребра: первое 10 см и второе 10 см, следовательно, площадь второй грани 10 · 10 = 100см². Затем Петрик так же измерил ребра тех граней, что остались, и нашел их площадь. Они оказались равными по 100 см².

- Теперь, - продолжал Петя, - добавим все эти площади и получим 600см². Это и будет площадь поверхности куба.

Как же он удивился, когда учитель не поставил ему высшей оценки. Как вы думаете, почему?

Последний фрагмент урока посвящен формированию понятия объем, единицы измерения объема и выведению формул объема прямоугольного параллелепипеда и куба.

@ Учителю, объясняя этот фрагмент материала, следует обратить внимание на то, что как и во время рассмотрения понятий о длину отрезка, площадь прямоугольника, так и в этом случае, измерения объектов начинается с договоренности о единице измерения.

Также ученики должны усвоить, что, в зависимости от длины ребра единичного куба, объем параллелепипеда будет выражаться разными числами и связь между ними можно записать в виде цепочки.

На закрепление этой части материала учащимся предлагается выполнить задание 6.

Выразите:

1) в кубических миллиметрах: 6 см³, 25 см³, 12 см³, 115 мм³, 1 дм³, 1 дм³ 25 см³ 6мм³;

2) в кубических дециметрах: 3 м³, 165 м³, 10 м³ 345 дм³, 15 м³ 13 дм³, 53000см³.

Задание 7. Найти объем фигур на рис. 148 учебника (с. 154), если они составлены из единичных кубиков, ребро которых равна 1 см.

После него учитель выводит формулы объема прямоугольного параллелепипеда и объем куба. (V = abc, V = а³ - название 3-й степени происходит именно с того, что третья степень числа а; выражает объем куба с ребром длиной а).

Ученики выполняют последнее задание.

Задача 8. Вычислите объем:

1) прямоугольного параллелепипеда с измерениями 12 м, 25 м и 4 м;

2) куба, длина ребра которого равна 3 м;

3) прямоугольного параллелепипеда, высота которого 12 см, длина - в 2 раза меньше высоты, а ширина на 2 см меньше длины;

4) куба, площадь поверхности которого равна 6 м².

III. Итог урока

Вопросы к классу:

1. Приведите примеры предметов, которые имеют форму прямоугольного параллелепипеда; куба.

2. Как называются: прямоугольники, из которых состоит прямоугольный параллелепипед, стороны граней прямоугольного параллелепипеда?

3. Геометрическое тело состоит из 25 кубиков с длиной ребра в 1 дм. Чему равен объем этого тела?

4. По каким формулам можно вычислять объем прямоугольного параллелепипеда, куба?

IV. Домашнее задание

п. 21, № 612; 614; 615; 617; 621; 625.