Урок № 59

Тема. Функция. Область определения и область значений функции

Цель: добиться осознания учащимися содержания понятий «функция», «функциональная зависимость», «область определения функции», «область значений функции, способы задания функции; осуществить первичное закрепление содержания изученных понятий; начать работу по выработке умений: а) задавать функциональные зависимости формулами; б) работать с функциями, заданными таблицей; в) вычислять по формуле значение функции, если известно значение аргумента и решать обратную задачу.

Тип урока: усвоение новых знаний.

Ход урока

I. Организационный момент

Учитель проверяет готовность учащихся к уроку.

@ Учитель сообщает ученикам о результатах тематической контрольной работы.

II. Проверка домашнего задания

1. Тетради с выполненным анализом тематической контрольной работы и коррекцией ученики сдают на проверку.

2. Работа с опережающим домашним заданием.

Задачи:

1) Составьте выражение для вычисления площади S квадрата со стороной а.

2) По составным выражением найдите S, если а = 1; 0,2; .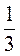

3) По составленной формуле найдите а, если S = 1; 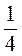; 0,25.

4) Каких значений могут принимать переменные S и а в выражении (если учесть, что а и S - длина стороны квадрата и его площадь соответственно)?

Ученики самостоятельно выполняют задания, делают записи:

1) Формула S = а2.

2) Если а = 1, то S = 12 = 1; если а = 0,2, то S = 0,22 = 0,04; если а = 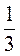, то .

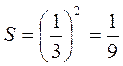3) S = 1, если а = 1; S = 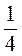, если а = 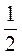; S = 0,25, если а = 0,5.

@ (Если у учащихся возникают трудности при выполнении этой части задания, следует показать им, что, во-первых, а по условию - сторона квадрата, поэтому может выражаться только положительным числом и, во-вторых, для нахождения а по известной S необходимо «подобрать такое число, чтобы выполнялось равенство а2 = S.)

4) Поскольку а - длина стороны, a S - площадь квадрата, то а > 0, S > 0.

После проверки полученных ответов, побуждаем учащихся к выводам, среди которых выделяем те, которые будут основой для формулировки цели урока формирование новых знаний учащихся, а именно:

5) зависимость (как толкуется в словаре):

Соотношение между двумя величинами может быть выражено формулой, причем эта формула помогает находить любую из этих двух величин через другую известную путем определенных вычислений.

Каждая из двух букв, входящих в формулу, может принимать значений, обусловленных, например, содержанием самих переменных.

Каждому значению одной переменной, входящей в состав формулы, может соответствовать единственное значение другой переменной.

Соотношению между переменными а и S в этом примере соответствует одно из значений слова «зависимость».

III. Формулировка цели и целей урока

Мотивация учебной деятельности

@ Слово учителя. Оказывается, что как и в повседневной жизни, так и в науке часто встречаются зависимости между двумя переменными, которые можно выразить формулами или другими способами, и свойства таких зависимостей очень похожи на тот пример, который мы рассмотрели. Поэтому на сегодняшнем уроке мы наконец выясним, как такие зависимости определяются в математике, математические понятия связанные с этим понятием, а также научимся решать контрольные задания на закрепление содержания обозначенных понятий.

IV. Актуализация опорных знаний

Выполнение устных упражнений

1. Площадь прямоугольника со сторонами 9 см и х см равна S см2. Выразите формулой зависимость S от х.

2. Поезд движется со скоростью 70 км/ч. За t часов он преодолевает S км. Задайте формулой зависимость S от t.

3. Пусть а см - длина ребра куба a V см3 - его объем. Задайте формулой зависимость V от а.

4. При каких значениях переменной имеет смысл выражение: 3 - х; ; ?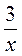

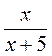V. Изучение нового материала

@ Содержание учебного материала по теме «Функция» до недавнего времени был обязательным для рассмотрения в 7 классе на уроках алгебры (последние несколько лет этот материал был перенесен до 8 класса). Традиционно функция трактуется как зависимость одной переменной от другой, при которой каждому значению одной переменной соответствует значение другой переменной Такой подход к введению понятия функции уже подготовлен рассмотрением различных примеров реальных зависимостей между величинами Учащиеся должны уяснить содержание понятий «область определения функции», «область значений функции», «аргумент» («независимая переменная»), «значение функции» («зависимая переменная»), постепенно они должны привыкнуть к высказываниям типа «Площадь квадрата является функцией его стороны» Полезно подчеркнуть, что термин «функция» используется в двух значениях - как сама зависимость и как значения зависимой переменной Также хотелось бы сказать, что учащиеся, имея все же склонность к предметному мышлению, лучше усваивают этот абстрактный материал, если подать достаточное количество примеров.

В этом месте курса алгебры, согласно новой Программе, выделяется отдельный вопрос «Способы задания функции» как специального предмета изучения Назад, объяснив, что задать функцию-значит указать способ, позволяющий для любого значения аргумента найти соответствующее значение функции, необходимо еще выделить, какие именно способы задания функции чаще всего используются на практике

План преподавания учебного материала можно предложить такой

1. Представление о зависимости (соответствие) между двумя переменными Независимая переменная Зависимая переменная.

2. Функциональные зависимости Функции Аргумент и значение функции.

3. Способы задания функции а) таблицей, б) формуле, в) графически, г) описание.

4. Область определения и область значений функции.

5. Пример Функция задана формулой у = 5х

1) Какая переменная является аргументом? [x] 2) Какая переменная является зависимой? [в]

3) Какое значение функции соответствует аргументу - 2?

[Если х = -2, то y = 5 ∙ (-2) = -10]

4) Какому значению аргумента соответствует значение функции у = 0,5? [в = 0,5, следовательно, 0,5 = 5х, х = 0,5 : 5]

Выводы. Две самые типичные задачи для функции по известному значению аргумента найти соответствующее значение функции - и обратным найти аргумент, что соответствует заданному значению функции.

VI. Первичное закрепление

Выполнение устных упражнений

1. Соответствия заданы таблицами

Какие из этих соответствий являются функциями?

Для функциональных зависимостей назовите пары соответствующих значений аргумента и функции Какова область определения этой функции? область значений каждой из этих функций?

Сможете ли вы задать эти функции формулой?

Выполнение письменных упражнений

1. Одна сторона прямоугольника равна 6 см, а вторая х см. По какой формуле можно вычислить площадь S прямоугольника? Задает ли эта форму и функцію9 Если да, укажите несколько значений ее аргумента и найдите по формуле соответствующие значения функции.

2. Автомобиль движется со скоростью 75 км/ч. За время t ч он преодолевает расстояние 5 км. Задайте зависимость между t и S формуле. Найдите значение функции, если t = 2,4 При каком значении аргумента функция принимает значение S = 150?

3. Функция задана формулой у = 2х2 + 1. Составьте таблицу значений функции для значений аргумента -4; -2; 0; 2; 4.

4. Функция задана формулой у = 4х - 5. Составьте таблицу значений аргумента, которым соответствуют значения функции 0; 3; 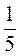; 0,7.

5. Функция задана таблицей

1) Найдите значение функции при х = -2; х = 2.

2) При каких значениях аргумента значение функции равно -1, 1?

3) Какова область определения функции?

4) Какова область значений функции?

5*) Каким уравнением можно было бы задать эту функцию?

VII. Итоги урока

Используя план урока (записан на доске), учащиеся обмениваются полученной информацией, выясняют, какая часть учебного материала была самой сложной, самой простой, какое понятие следует доработать дома

VIII. Домашнее задание

Изучите определение основных понятий урока, выполните задания:

№1 Функция задана формулой у = 2х2 - 7х + 1. Найдите значение функции, соответствующее значению аргумента 1; -2; 0,3; 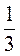; 0.

№ 2. Функция задана формулой у = 0,1 х + 5. Для значения аргумента, равном 10; 50; 120 отыщите соответствующие значения функции.

№ 3. Опережающее домашнее задание.

1) За учебником или конспектом повторите, что такое область допустимых значений.

Найдите ОДЗ выражения .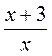

2) Пусть функция задана формулой .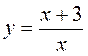

Можно найти значение функции, если аргумент равен -5; -3; 0. Почему? Какое из приведенных чисел не будет входить в область определения функции? Сравните свой ответ с п. 1). Сделайте выводы.
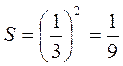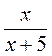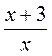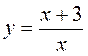