УРОК № 60
Тема. Тематическая контрольная работа № 7
Цель урока: проверка учебных достижений учащихся по курсу геометрии.
Тип урока: контроль учебных достижений учащихся.
Требования к уровню подготовки учащихся: применяют определения и свойства фигур при решении задач.
Ход урока
И. Тематическое оценивание № 7
Тематическое оценивание № 7 можно провести в виде тематической контрольной работы. Приводим текст контрольной работы. Каждый правильный ответ оценивается в 3 балла.
Вариант 1
- 1. Боковая сторона остроугольного равнобедренного треугольника равна 25 см, а высота, опущенная на нее, - 24 см. Найдите периметр треугольника.
- 2. Диагонали ромба равны 30 см и 40 см. Найдите высоту ромба.
- 3. Радиус круга, описанного вокруг прямоугольного треугольника, равна 10 см, а катет - 16 см. Найдите площадь вписанного круга.
- 4. Найдите |
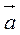 -
- 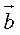 |, если |
|, если |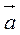 | = 7, |
| = 7, |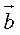 | = 8, a угол между векторами
| = 8, a угол между векторами 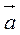 и
и 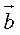 равен 120°.
равен 120°.
Вариант 2
- 1. Основание остроугольного равнобедренного треугольника равно 30 см, а высота, опущенная на боковую сторону, - 24 см. Найдите периметр треугольника.
- 2. Сторона ромба равна 25 см, а его высота - 24 см. Найдите диагонали ромба.
- 3. Радиус круга, вписанного в прямоугольный треугольник, равен 4 см, а катет - 12 см. Найдите площадь описанного круга.
- 4. Найдите |
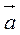 +
+ 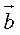 |, если |
|, если |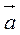 | = 7, |
| = 7, |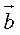 | = 8, а угол между векторами
| = 8, а угол между векторами 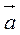 и
и 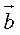 равен 60°.
равен 60°.
Вариант 3
- 1. Периметр равнобедренного треугольника равен 80 см, а высота, опущенная на основание - 20 см. Найдите основание треугольника.
- 2. Сторона ромба равна 12
 см, а тупой угол составляет 120°. Найдите диагонали ромба.
см, а тупой угол составляет 120°. Найдите диагонали ромба.
- 3. Точка касания вписанной в прямоугольный треугольник круга делит гипотенузу на отрезки длиной 8 см и 12 см. Найдите площадь вписанного круга.
- 4. Найдите |
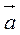 -
- 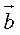 |, если |
|, если |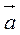 | = 3, |
| = 3, |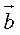 | = 8, а угол между векторами
| = 8, а угол между векторами 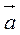 и
и 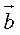 равен 60°.
равен 60°.
Вариант 4
- 1. Периметр равнобедренного треугольника равна 160 см, а высота, опущенная на его основание - 40 см. Найдите боковую сторону треугольника.
- 2. Диагонали ромба равны 12 см и 12
 см. Найдите острый угол ромба.
см. Найдите острый угол ромба.
- 3. Точка касания вписанной в прямоугольный треугольник окружности делит его гипотенузу в отношении 2 : 3. Катет равен 12 см. Найдите площадь вписанного круга.
- 4. Найдите |
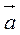 +
+ 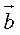 |, если |
|, если |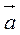 | = 5, |
| = 5, |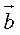 | = 8, а угол между векторами а и b составляет 120°.
| = 8, а угол между векторами а и b составляет 120°.
Решения и ответы к заданиям тематической контрольной работы № 7
Вариант 1
1. Ответ. 80 см.
2. Ответ. 24 см.
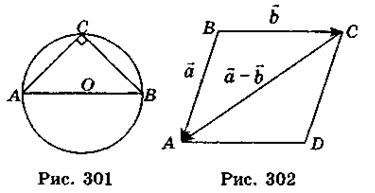
3. Пусть треугольник ABC прямоугольный, АО = 10 см, ВС = 16 см (рис. 301).
Из прямоугольного треугольника ABC имеем: АС =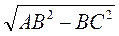 =
=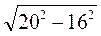 = 12 (см). r =
= 12 (см). r = 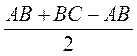 =
= 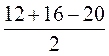 = 4(см). Sкр = nr2 = n · 42 = 16n (cм2).
= 4(см). Sкр = nr2 = n · 42 = 16n (cм2).
Ответ. 16n см2.
4. Пусть ВА = 7, ВС = 8,  ABC = 120° (рис. 302).
ABC = 120° (рис. 302).
|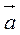 -
- 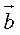 | = АС =
| = АС = 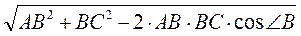 =
= 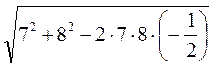 =
= 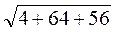 = 13.
= 13.
Ответ. 13.
Вариант 2
1. Ответ. 80 см.
2. Ответ. 30 и 40 см.
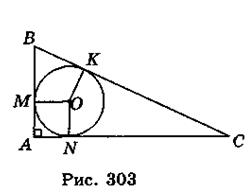
3. Пусть в прямоугольный треугольник ABC ( A = 90°) вписан круг; М, N, К - точки касания, OM = ON = OK = 4 см, АВ = 12 см (рис. 303).
A = 90°) вписан круг; М, N, К - точки касания, OM = ON = OK = 4 см, АВ = 12 см (рис. 303).
Тогда ВМ = АВ - АМ = 12 - 4 = 8 (см), ВК = 8 см.
Пусть КС = х см. Тогда ВС = х + 8, АС = х + 4 и с треугольника ABC имеем:
(х + 8)2 = (х + 4)2 + 122; х2 + 16х + 64 = х2 + 8х + 16 + 144; 8х = 96, х = 12. Следовательно, ВС = 12 + 8 = 20 (см). S = nR2 = n · 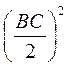 = n · 102 = 100n (см2).
= n · 102 = 100n (см2).
Ответ. 100n см2.
4. Пусть |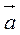 | = АВ = 7, |
| = АВ = 7, |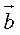 | = AD = 8,
| = AD = 8,  BAD = 60° (рис. 304), тогда
BAD = 60° (рис. 304), тогда  ABC = 180° - 60° = 120°. Из треугольника ABC имеем:
ABC = 180° - 60° = 120°. Из треугольника ABC имеем:
|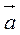 +
+ 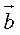 | = АС =
| = АС = 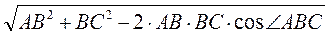 =
= 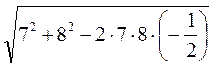 =
= 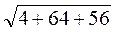 = 13.
= 13.
Ответ. 13.
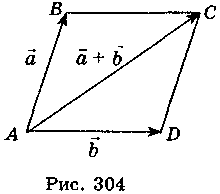
Вариант 3
1. Ответ. 30 см.
2. Ответ. 12 см и 36 см.
см и 36 см.
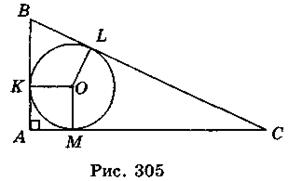
3. Пусть в прямоугольный треугольник ABC вписан круг, М, L, К - точки касания; BL = 8 см, CL = 12 см (рис. 305). ВК = KL = 8 см, LC = MC = 12 см.
Пусть АК = х см, тогда АМ = х см. Итак, из треугольника ABC имеем:
(х + 8)2 + (х + 12)2 = 202; х2 + 16х + 64 + х2 + 24х + 144 = 400;
2х2 + 40х - 192 = 0, х2 + 20х - 96 = 0 , х = -24 или х = 4. х = -24 условие задачи не удовлетворяет, следовательно, х = 4 см. S = n · AM2 = n · 42 = 16n (см2).
Ответ. 16n см2.
4. Пусть |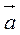 | = АВ = 3, |
| = АВ = 3, |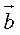 | = АО = 8,
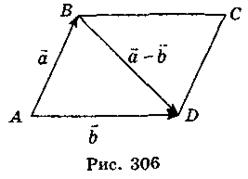
| = АО = 8,  BAD = 60° (рис. 306).
BAD = 60° (рис. 306).
|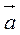 -
- 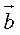 | = BD =
| = BD = 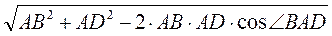 =
= 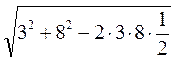 =
= 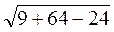 = 7.
= 7.
Ответ. 7.
Вариант 4
1. Ответ. 50 см.
2. Ответ. 60°.
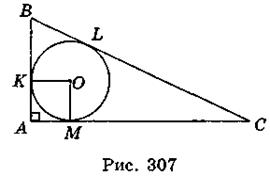
3. Пусть в прямоугольный треугольник ABC ( A = 90°) вписан круг; К, L, М - точки касания, АВ = 12 см, BL : CL = 2 : 3 (рис. 307).
A = 90°) вписан круг; К, L, М - точки касания, АВ = 12 см, BL : CL = 2 : 3 (рис. 307).
Пусть АК = х см, тогда ВК = 12 - х, BL = 12 - x, LC = 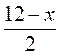 · 3 = 18 - 1,5х,
· 3 = 18 - 1,5х,
BC = BL + LC = 30 - 2,5 x, АС = х + 18 - 1,5 х = 18 - 0,5 х. Из прямоугольного треугольника ABC имеем: (30 - 2,5 х)2 = 122 + (18 - 0,5x)2;
900 - 150х + 6,25х2 = 144 + 324 - 18х + 0,25х2; 6х2 - 132х + 432 = 0, х2 - 22х + 72 = 0, х = 18 х = 4.
Учитывая, что х 12, имеем х = 4. Итак, ОК = 4 см. S = n · OK2 = 16n (см2).
Ответ. 16n см2.
4. Пусть |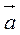 | = АВ = 5, |
| = АВ = 5, |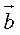 | = BC = 8,
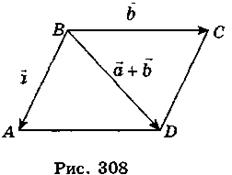
| = BC = 8,  АВС = 120° (рис. 308).
АВС = 120° (рис. 308).
Тогда  BCD = 180° - 120° = 60°. Из треугольника BCD имеем:
BCD = 180° - 120° = 60°. Из треугольника BCD имеем:
|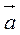 +
+ 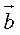 | = BD =
| = BD = 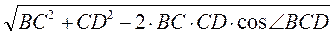 =
= 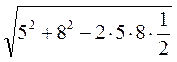 =
= 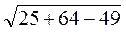 = 7.
= 7.
Ответ. 7.
Тематическое оценивание № 7 можно провести в виде тестового задания. Каждое задание i И II уровней оценивается 1 баллом, III уровня - 2 балла, IV уровня - 3 баллами.
При оценивании учитываются только те шесть из выполненных заданий, которым соответствует наибольшее количество баллов. Если ученик набрал в сумме нецілу количество баллов, результат округляется в сторону увеличения; если больше 12 баллов - получает 12 баллов.
Тестовая работа
И уровень
- 1. В прямоугольном треугольнике ABC (
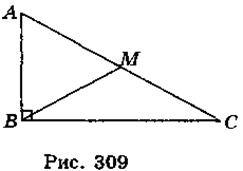
 B = 90°) проведена меде ану ВМ (рис. 309). Выберите правильное утверждение.
B = 90°) проведена меде ану ВМ (рис. 309). Выберите правильное утверждение.
A.  A +
A +  C = 90°;
C = 90°;
Б. М - центр окружности, вписанной в треугольник ABC;
В. АМ > ВМ.
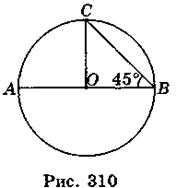
- 2. Если диаметр АВ окружности с центром в точке А образует с хордой ВС угол 45° (рис. 310), то градусная мера угла АОС равна:
А. 45°; Б. 60°; В. 90°.
- 3. Если ABCD - прямоугольник (рис. 311), то:
A. AC BD;
BD;
Б. АС2 > АВ2 + ВС2;
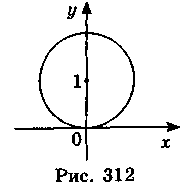
В.  АСВ
АСВ 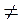
 ACD.
ACD.
II уровень
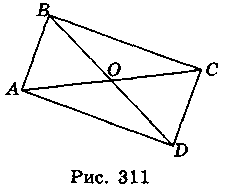
- 4. Укажите уравнение окружности, изображенной на рис. 312.
A. (x - 1)2 + y2 = 1;
Б. х2 + (у - 1)2 = 1;
В. (x + 1)2 + y2 = 1.
- 5. Если квадрат описан около окружности радиуса r, то площадь квадрата равна:
А. r2; Б. 2r2; В. 4r2.
- 6. Если круг вписан в квадрат со стороной 2а, то площадь круга равна:
А. 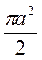 ; Бы. nа2; В. 2nа2.
; Бы. nа2; В. 2nа2.
III уровень
- 7. Гипотенуза прямоугольного треугольника равна 10 см, а один из катетов равен 6 см. Найдите площадь треугольника.
А. 24 см2; Б. 48 см2; В. 60 см2.
- 8. Проекции катетов прямоугольного треугольника на гипотенузу соответственно равны 9 см и 16 см. Найдите меньший катет треугольника.
А. 12 см; Б. 15 см; В. 20 см.
- 9. Найдите площадь ромба, сторона которого равна 13 см, а разность диагоналей составляет 14 см.
А. 60 см2; Б. 120 см2; В. 240 см2.
IV уровень
- 10. В треугольнике два угла составляют 120° и 30°, а прилегающая к ним сторона равна 10 см. Найдите высоту треугольника, проведенную к стороне длиной 10 см.
А. 5 см; Б. 5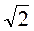 см; В. 5
см; В. 5 см.
см.
- 11. В ромб вписан круг. Сторона ромба точкой касания делится на отрезки, длины которых равны а и b. Найдите площадь ромба.
А. 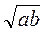 ; Бы. 2
; Бы. 2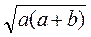 ; В. 2
; В. 2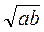 (а + b).
(а + b).
- 12. Точки А(-2; 0), В(2; 4), С(4; 2), D(0; -2) - вершины четырехугольника ABCD. Найдите координаты центра круга, описанного вокруг него.
А. (2; 0); Б. (1; 0); B. (1; 1).
Ответы к заданиям тестовой работы
1. А. 2. В. 3. В. 4. Б. 5. В. 6. Б. 7. А. 8. Б. 9. Б. 10. В. 11. В. 12. В.
II. Домашнее задание
Если в классе выполнялась тематическая контрольная работа № 7, то дома можно предложить выполнить тест, и наоборот.
III. Подведение итогов урока
Выяснить, какие задания вызвали затруднения у учащихся, и ответить на вопросы учеников.