УРОК № 59

Тема. Тематическая контрольная работа № 6

Цель урока: проверка знаний учащихся по теме «Начальные сведения из стереометрии».

Тип урока: контроль учебных достижений учащихся.

Требования к уровню подготовки учащихся: применяют определения и свойства геометрических фигур при решении задач.

Ход урока

И. Тематическое оценивание № 6

Тематическое оценивание № 6 можно провести в виде тематической контрольной работы. Приводим текст контрольной работы. Каждый правильный ответ оценивается в 3 балла.

Вариант 1

1. 1. В основе пирамиды лежит квадрат со стороной 5 см. Вычислите объем пирамиды, если ее высота равна 6 см.
2. 2. В основании правильной призмы лежит треугольник со стороной 4 см, а ее боковое ребро равно 10 см. Найдите площадь боковой поверхности этой призмы.
3. 3. Диагональ осевого сечения цилиндра равна 10 см, а его высота - 6 см. Найдите площадь поверхности и объем цилиндра.
4. 4. Образующая конуса равна l и образует с высотой конуса угол α. Найдите площадь боковой поверхности и объем конуса.

Вариант 2

1. 1. В основании прямой треугольной призмы лежит прямоугольный треугольник с катетами 3 см и 4 см. Вычислите объем призмы, если ее боковое ребро равно 5 см.
2. 2. Найдите площадь поверхности треугольной пирамиды, если каждое из его ребер равна 6 см.
3. 3. Радиус основания конуса равен 6 см, а его высота - 8 см. Найдите площадь поверхности и объем конуса.
4. 4. Диагональ осевого сечения цилиндра равна l и образует с образующей цилиндра угол α. Найдите площадь боковой поверхности и объем цилиндра.

Вариант 3

1. 1. Высота цилиндра равна 6 см, а диаметр основания - 8 см. Найдите площадь боковой поверхности цилиндра.
2. 2. Образующая конуса равна 5 см, а его высота - 4 см. Найдите объем конуса.
3. 3. В основании правильной пирамиды лежит квадрат со стороной 10 см. Высота пирамиды равна 12 см. Найдите площадь поверхности и объем пирамиды.
4. 4. Диагональ боковой грани правильной треугольной призмы равна l и образует с боковым ребром угол α. Найдите площадь боковой . поверхности и объем призмы.

Вариант 4

1. 1. Диаметр основания конуса равен 6 см, а образующая - 5 см. Найдите площадь боковой поверхности конуса.
2. 2. Диагональ осевого сечения цилиндра равна 13 см, а его высота 5 см. Найдите объем цилиндра.
3. 3. В основе прямой призмы лежит прямоугольный треугольник с катетами 6 см и 8 см. Боковое ребро равняется наибольшему ребру основания. Найдите площадь поверхности и объем призмы.
4. 4. Боковое ребро правильной четырехугольной пирамиды равна l и образует с высотой угол α. Найдите площадь боковой поверхности и объем пирамиды.

Ответы и решения к заданиям тематической контрольной работы

Вариант 1

1. V = 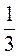Sосн Н. Поскольку Sосн = 52 = 25(см2), Н = 6 см, то V = 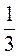∙ 25 ∙ 6 = 50 (см3). Ответ. 50см3.

2. Sбоков = P ∙ H. Поскольку Р = 3 ∙ 4 = 12 (см), Н = 10 см, то Sбоков = 12 ∙ 10 = 120 (см2). Ответ. 120 см2.

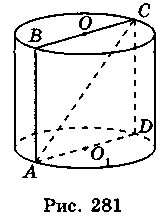
3. Пусть АС = 10 см, CD = 6 см (рис. 281), тогда из треугольника ACD имеем:

AD = 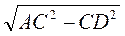= = 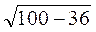8 (см), следовательно, АО = 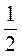AD = 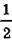∙ 8 = 4 (см).

S = Sбоков + 2Sосн = 2n ∙ AО1 ∙ CD + 2n ∙ AO12 = 2n ∙ 4 ∙ 6 + 2n ∙ 42 = 48n + 32n = 80n (см2). V = nАО12 ∙ CD = n ∙ 42 ∙ 6 = 96n (см3).

Ответ. 80n см2, 96n см3.

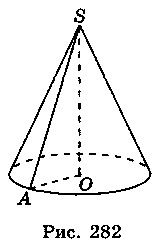
4. Пусть AS = l, ASO = α (рис. 282). Тогда из треугольника ASO имеем:

АО = AS sinASO = l sinα, SO = AS cosASO = lcosα.

Sбоков = n ∙ AO ∙ AS = n l sinα ∙ l = nl2sinα.

V = 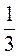n ∙ AO2 ∙ SO = 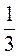nl2 sin2α l cosα = .

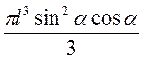Ответ. nl2sinα, .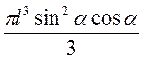

Вариант 2

1. V = Sосн · H. Поскольку S = 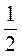· 3 · 4 = 6 (см2), Н = 5 см, то V = 6 · 5 = 30 (см3). Ответ. 30 см3.

2. S = 4 · SΔ = 4 · 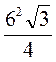= 36 (см2). Ответ. 36 см2.

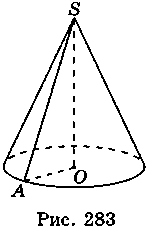
3. Пусть AО = 6 см, SO = 8 см (рис. 283), тогда из треугольника SAO имеем:

AS = 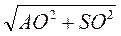= = 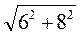10 (см).

Sкон = Sосн + Sбоков = n · AО2 + n · AO · AS = n · 62 + n · 6 · 10 = 96n (см2).

V = 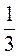n · AO2 · SO = 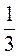n · 62 · 8 = 96n (см3). Ответ. 96n см2 , 96n см3.

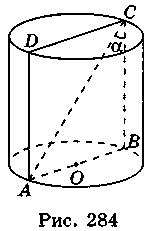
4. Пусть AC = l, ACB = α (рис. 284). Тогда из треугольника АСВ имеем:

СВ = AC cosАСВ = l cosα, АВ = AC sinАСВ = l sinα,

отсюда АО = 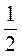АВ = 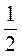l sinα.

Sбоков = 2n · АО · СВ = 2 · n · 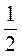lsinα · lcosα = nl2 sinα cosα.

V = n · AO2 · CB = n · 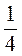l2 sin2α · lcosα = .

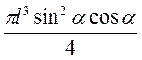Ответ. nl2 sinα cosα, .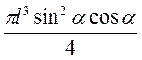

Вариант 3

1. Sбоков = 2nRH. Поскольку 2R = 8 см, H = 6 см, то Sбоков = n · 8 · 6 = 48n (см2).

Ответ. 48n см2.

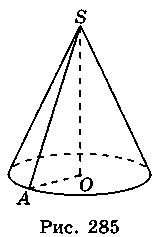
2. Пусть AS = 5 см, SO = 4 см (рис. 285). Тогда из треугольника SAO имеем:

АО = 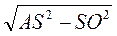= = 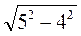3 (см).

V =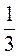n · A2 · SO = 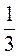n · 9 · 4 = 12n (см3). Ответ. 12n см3.

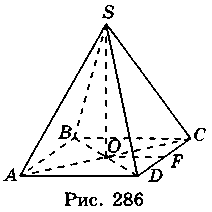
3. Пусть SABCD - правильная пирамида, АВ = 10 см, SO = 12 см (рис. 286). Проведем SF CD, тогда DF = CF = 5 см. Из прямоугольного треугольника SOF имеем: SF = 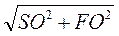= =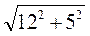13 (см).

S = Sосн + Sбоков = AB2 + 2 · AB · SF = 102 + 2 · 10 · 13 = 360 (см2).

V = 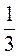AB2 · SO = 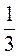· 100 · 12 = 400 (см3). Ответ. 360 см2, 400 см3.

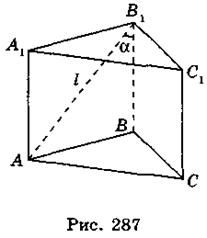
4. Пусть ABCA1В1C1 - прямая призма, в которой АВ1 = l, AB1B = α (рис. 287). Из прямоугольного треугольника АВ1В имеем: АВ = АВ1 sinАB1В = l sinα, BB1 = АВ1 cosAB1B = l cosα.

Sбоков = 3 · АВ · ВВ1 = 3 · l sinα · l cosα = 3l2sinαcosα.

V = Sосн · BB1 = 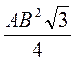· BB1= 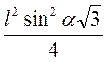· 2cosα = .

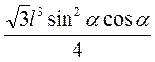Ответ. 3l2 sinα cosα, .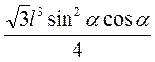

Вариант 4

1. Sбоков = nRl. Поскольку R = 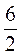= 3 (см), l = 5 см. то Sбоков = n · 3 · 5 = 15π (см2).

Ответ. 15n см2.

2. Пусть AC = 13 см, CD = 5 см (рис. 288). Тогда из прямоугольного треугольника ACD имеем: AD = 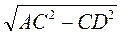= = 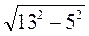12 (см),

АО = 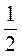AD = 6 (см). V = n · АО2 · СD = n · 62 · 5 = 180n (см3).

Ответ. 180n см3.

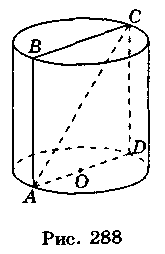
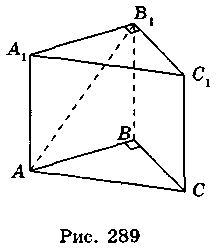
3. Пусть АВСA1В1C1 - прямая призма, B = 90°, AB = 6 см, ВС = 8 см, АА1 = АС (рис. 289). Из треугольного треугольника ABC имеем:

АС = 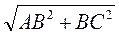= = 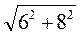10 (см).

S = 2Sосн + Sбоков= 6 · 8 + 24 · 10 = 48 + 240 = 288 (см2).

V = Sосн · AA1 = 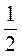· AB · BC · AA1 = 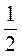· 6 · 8 · 10 = 240(см3).

Ответ. 288 см2, 240 см3.

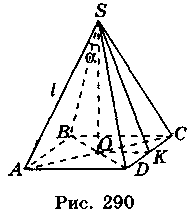
4. Пусть SABCD - правильная пирамида, AS = l, ASO = α (рис. 290). Из прямоугольного, треугольника SOA имеем:

АО = AS sinASO = l sinα, SO = AS cosa ASO = l cosα.

Тогда AB = DC = AO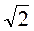= 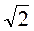l sinα.

Проведем SK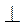SC, тогда SK = 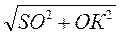= = 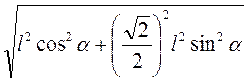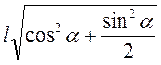. Sбоков = 2 · DC · SK = 2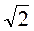lsinα · l· 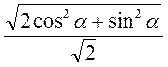= 2l2 sinα .

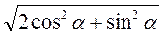V = 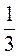AB2 · SO = 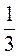· 2l2sin2α · lcosα = .

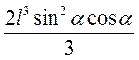Ответ. 2l2sinα, .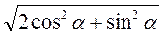

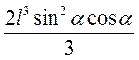Тематическое оценивание № 6 можно провести в виде теста.

Тестовая работа

Каждое задание i И II уровней оценивается 1 баллом, III уровня - 2 балла, IV уровня - 3 баллами. При оценивании учитываются только те шесть из выполненных заданий, которым соответствует наибольшее количество баллов. Если ученик набрал в сумме нецілу количество баллов, результат округляется в сторону увеличения. Если ученик набрал 12 баллов, он получает 12 баллов.

Вариант 1

I уровень

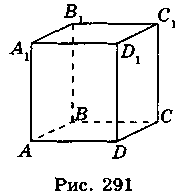
1. 1. На рис. 291 изображен куб ABCDA1B1C1D1. Какой из указанных прямых параллельна прямой ВС?

А DС1 Б АА1 В A1D1

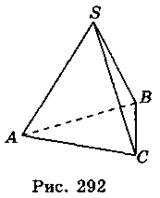
1. 2. На рис. 292 изображена пирамида SABC. Какой из указанных прямых мимобіжна прямая SB?

A. AS; Б. АС; В. АВ.

1. 3. Укажите, какие из приведенных утверждений являются правильными.
   А. Треугольная пирамида имеет три грани;

Б. Треугольная пирамида имеет четыре ребра;

В. Противоположные ребра треугольной пирамиды не пересекаются.

II уровень

1. 4. Радиус шара равен 6 см. Найдите площадь поверхности шара.

А. 144n см2; Б. 288n см2; В. 576n см2.

1. 5. Каждое ребро правильной треугольной призмы равна 6 см. Найдите объем призмы.

А. 9(см3); Б. 12(см3); В. 36(см3).

1. 6. Радиус основания конуса равен 3 см, а образующая - 5 см. Найдите высоту конуса.

А. 3 см; Б. 4 см; В. 5 см.

III уровень

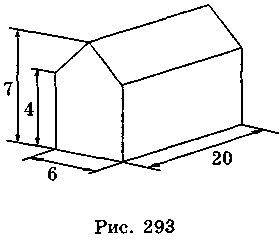
1. 7. Стог сена имеет форму прямой призмы с пятиконечной основой (рис. 293). Размеры скирды (в метрах) представлена на рисунке. Найдите объем скирды.

А. 330 м3; Бы. 600 м3; В. 660 м3.

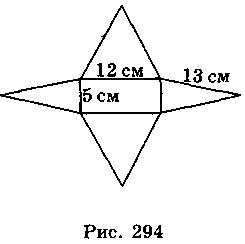
1. 8. На рис. 294 изображен развертку четырехугольной пирамиды, в основании которой лежит прямоугольник со сторонами 5 см и 112 см, а боковые грани которой - равнобедренные треугольники, с боковой стороной 13 см. Найдите объем пирамиды.

А. 130 см3; Бы. 130см3; В. 390 см3.

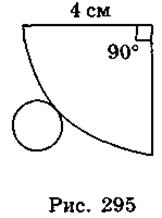
1. 9. На рис. 295 изображен развертку конуса. Найдите площадь боковой поверхности конуса.

А. 2n см2; Б. 4n см2; В. 12n см2.

IV уровень

1. 10. Цилиндр образован при вращении прямоугольника вокруг стороны, которая образует с диагональю а прямоугольника угол α. Найдите объем цилиндра.

A. nd3 sinα cosα;

Б. nd3 sinα cosα;

В. nd3 sinα cosα.

1. 11. В основе прямой призмы лежит квадрат. Диагональ призмы равна d и образует с боковым ребром угол α. Найдите объем призмы.

A. 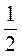d3 sin2α;

Б. 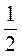d3 sin2α cosα;

B. 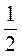d3 sin2α cosα.

1. 12. В основе пирамиды лежит ромб со стороной l и острым углом α. Высота пирамиды равна Н, основание высоты пирамиды является точкой пересечения диагоналей ромба. Найдите объем пирамиды.

A. 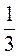Hl2 sinα;

Б. 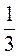H2l sinα;

В. 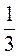Нl2 cosα.

Вариант 2

И уровень

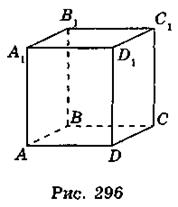
1. 1. На рис. 296 изображен куб ABCDA1B1C1D1. Какой из указанных прямых параллельна прямой АВ?

A. DC1; Б. D1С1; В. CC1.

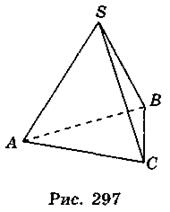
1. 2. На рис. 297 изображена пирамида SABC. Какой из указанных прямых мимобіжна прямая АВ?

A. SA; БЫ. SB; В. SC.

1. 3. Укажите, какие из приведенных утверждений являются правильными.
   А. Куб имеет шесть ребер;

Б. Все ребра куба равны;

В. Куб имеет двенадцать вершин.

II уровень

1. 4. Радиус шара равен 6 см. Найдите объем шара.

А. 144n см3; Б. 288n см3; В. 576n см3.

1. 5. Каждое ребро треугольной пирамиды равна 6 см. Найдите площадь поверхности пирамиды.

А. 9 см2; Б. 36см2; В. 72см2.

1. 6. Радиус основания цилиндра равен 3 см, а высота цилиндра 4 см. Найдите площадь боковой поверхности цилиндра.

А. 9n см2; Б. 18n см2; В. 24n см2.

III уровень

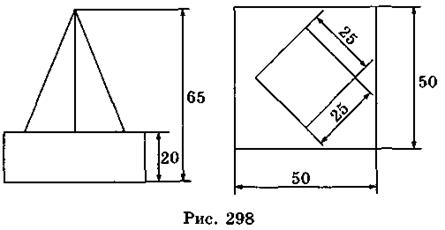
1. 7. 7. На рис. 298 изображены две проекции детали (вид спереди и сверху). Размеры представлены в миллиметрах. Найдите объем детали.

А. 50 см3; Бы. 53,125 см3; В. 60 см3.

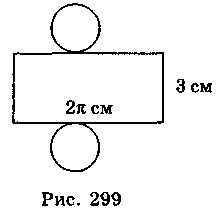
1. 8. На рис. 299 изображен развертку цилиндра. Найдите объем цилиндра.

А. 3n см3; Бы. 6n см3; В. 18n см3.

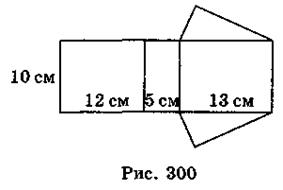
1. 9. На рис. 300 изображено развертку прямой треугольной призмы. Найдите площадь поверхности призмы.

А. 600 см2; Б. 300 см2; В. 360 см2.

IV уровень

1. 10. Конус образован при вращении прямоугольного треугольника вокруг катета, равна а и образует угол α с гипотенузой. Найдите объем конуса.

А. 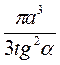; Бы. 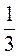na3tg2α; В. 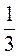na3sin2α.

В основе прямой призмы лежит прямоугольный треугольник с гипотенузой с и острым углом α. Боковое ребро призмы равна наибольшей стороне основания призмы. Найдите объем призмы.

A. 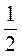c3 sinα cosα;

Б. 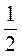с3 sinα cosα;

B. 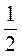c3 sinα cos2α.

1. 11. В основе пирамиды лежит равнобедренный треугольник с боковой стороной l и углом при вершине α. Высота пирамиды равна Н, основание высоты пирамиды - центр окружности, описанной вокруг основания пирамиды. Найдите объем пирамиды.

A. 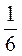H2l sinα;

Б. 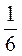Hl2 sin2α;

В. 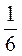Нl2 sinα.

Ответы к заданиям тестовой работы

II. Домашнее задание

Если в классе выполнялась тематическая контрольная работа № 5, то дома можно предложить выполнить тест, и наоборот.

III. Подведение итогов урока

Выяснить, какие задания вызвали затруднения у учащихся, и ответить на вопросы учеников.
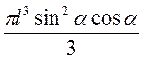
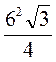
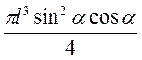
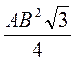
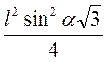
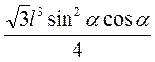
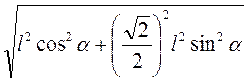
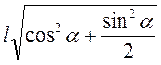
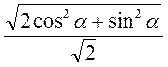
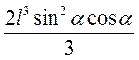
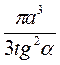