|
@ В изучении материала урока следует обратить внимание учащихся на следующие ключевые моменты: во-первых, общий план решения задач с помощью уравнений, изученный в 7 классе, «работает» и для случая, когда уравнение, соответствующее условию задачи, является нелинейным (квадратным, дробным...). Во-вторых, процесс решения задачи составлением уравнения представляет собой своего рода замкнутый цикл (задача → математическая модель задачи → решение математической модели → интерпретация решения согласно условия задачи), то есть за развязыванием уравнение обязательно должно идти интерпретация найденных корней уравнения согласно условия задачи. При условии, что учащиеся имеют достаточно высокий уровень учебных достижений, после рассмотрения примеров задач на составление квадратного уравнения можно обобщить сведения о видах задач, которые можно решать составлением квадратного уравнения.
VI. Формирование умений Выполнение письменных упражнений Для реализации дидактической цели урока следует решить задачи следующего содержания: 1. Арифметические задачи на составление квадратного уравнения. 1) Произведение двух чисел равна 135. Найдите эти числа, если одно из них на 6 больше другого. 2) Разность двух положительных чисел равна 23, а их произведение равно 420. Найдите эти числа. 3) Произведение двух натуральных чисел, одно из которых на 6 больше второго, равен 187. Найдите ни числа. 4) Произведение двух последовательных натуральных чисел больше их сумму на 109. Найдите эти числа. 2. Геометрические задачи на составление квадратного уравнения (на применение теоремы Пифагора, применение понятие площади прямоугольника, квадрата). 1) Найдите стороны прямоугольника, периметр которого равен 30 см, а площадь - 56 см2. 2) Найдите периметр прямоугольника, длина которого на 4 см больше ширины, а плота равна 60 см2. 3) От листа картона, имеющего форму квадрата, отрезали полосу шириной 3 см. Площадь прямоугольной части листа, что осталась, равна 70 см2. Определите первоначальные размеры листа. 3. На повторение: задачи на прямолинейное равномерное движение, сводящиеся к линейным уравнениям. Из А в В со скоростью 12 км/ч выехал велосипедист, а через полчаса вслед за тем выехал мотоциклист со скоростью 48 км/ч. Мотоциклист прибыл в В на 1 ч 15 мин раньше велосипедиста. Какое расстояние АВ? 4. Логические упражнения и задачи повышенного уровня сложности для учащихся, имеющих достаточный и высокий уровни знаний. 1) На соревнованиях по баскетболу было сыграно 45 игр. Сколько команд приняли участие в соревнованиях, если каждая команда сыграла со всеми другими по одному разу? 2) Есть лист картона прямоугольной формы, длина которого в 1,5 раза больше его ширины. Из него можно изготовить открытую коробку объемом 6080 см3, вырезав по углам картона квадраты со стороной 8 см. Найдите размеры - длину и ширину листа картона. 3) Найдите пропущенное число:
5. На повторение: упражнения на решение дробно-рациональных уравнений. 1) Решите уравнение: а) б) в) г) 2) Найдите значение переменной у, при которых: а) сумма дробей б) сумма дробей в) разность дробей
VII. Итоги урока В каком случае правильно выполнено записи? 1. Условию задачи: «Одно число х, а второе па 3 больше, их произведение равно 88» соответствует уравнение: а) х(х - 3) = 88; б) х + (х + 3) = 88; в) х(х + 3) = 88; г) х - (х + 3) = 88. 2. Условию задачи: «Площадь прямоугольника равна 32 см2, сумма смежных сторон - 12 см. Найти стороны прямоугольника» соответствует уравнение: а) х + 32 = х + 12; б) х(12 + х) = 32; в) VIII. Домашнее задание 1. Изучить (повторить) схему решения задач с помощью квадратных уравнений. 2. Решить задачи на составление квадратных уравнений. 3. На повторение: упражнения на решение дробно-рациональных уравнений, задачи на движение на составление целого уравнения с одной переменной (7 класс).
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

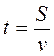 ,
, 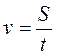 ,
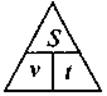
,
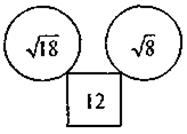
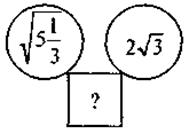
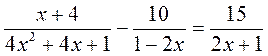 ;
; 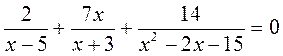 ;
;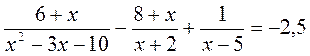 ;
; 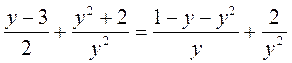 .
.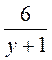 и
и 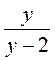 равна их произведению;
равна их произведению;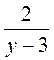 и
и 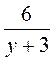 равна их доле;
равна их доле;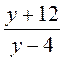 и
и 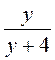 равна их произведению.
равна их произведению.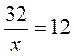 ; г
; г