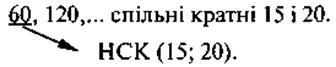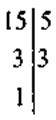Урок № 6

Тема. Наименьшее общее кратное нескольких натуральных чисел

Цель: на основе знаний об кратное число сформировать представление учащихся о понятии общего кратного нескольких натуральных чисел, НСК, а также научить их пользоваться алгоритмом нахождения нок двух (трех и т.д.) натуральных чисел.

Тип урока: усвоение новых знаний.

Ход урока

И. Проверка домашнего задания

@ Для более интересного протекания процесса проверки домашнего задания на уроке можно предложить ученикам провести эту работу в игровой форме, например в виде игры «Найди ошибку». (Учитель заранее записывает на доске решение упражнений домашней работы, совершив несколько типичных ошибок. Ученики, проверяя написанное, должны найти ошибку; можно организовать соревнование: кто найдет большее количество ошибок и сумеет их объяснить.)

Для «слабых» учеников, домашнее задание которых учитель проверяет перед уроком, в это время можно предложить работу с карточками-подсказками.

II. Актуализация опорных знаний

Вопрос к классу

1. Известно, что а, b, с - натуральные числа и а = bс. Как можно назвать число а по отношению к b? по отношению к а?

2. Назовите самые маленькие три натуральных числа, кратных 2; 5; а.

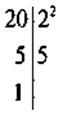
III. Формирование новых знаний

@ Подходы к преподаванию темы НСК и НОД очень похожи, поэтому этот этап урока проводится аналогично соответствующего этапа предыдущего урока.

1. Постановка проблемы

Задача. В киоск завезли тетради. Если разложить по 15 тетрадей или по 20 тетрадей в пачку, то в обоих случаях лишних тетрадей не останется. Которую (наименьшее) количество тетрадей могли завезти в киоске? Какое наименьшее количество тетрадей могла быть завезена?

Анализ условия приводит к выводу, что во время решения задачи надо найти числа, которые делятся (кратные) на 15 и на 20.

2. Решение проблемы

Учащиеся знакомятся с понятиями:

· общее кратное нескольких натуральных чисел, наименьшее общее кратное (НОК);

· алгоритм нахождения НСК нескольких чисел.

Короткие заметки можно оформить в виде конспекта:

Решение задачи: НСК(15; 20) = 60, следовательно, наименьшее количество тетрадей 60; возможные варианты 120, 180, 60n тетрадей.

IV. Закрепление знаний и формирование умений

И уровень

Устные упражнения

1. Какое число называют общим кратным а и b?

2. Какое число называют НСК чисел а и b?

3. Найдите НСК(а; b), если:

а) а = 3·5; b = 1;

б) а = 3·5; b = 5·7;

в) а = 32·5; b = 3·5.

II уровень

Письменные упражнения

1. Найдите наименьшее общее кратное чисел а и b, если:
a) a = 22·3·52; b = 2·33·5;

б) а = 32·72; b = 2·3·3·5·7·7;
в) а = 2·2·5·5·11; b = 2·2·3·5·11.

2. Найдите наименьшее общее кратное чисел:
а) 6 и 8; б) 72 и 99; в) 396 и 180; г) 34; 51 и 68.

3. В портовом городе начинаются три туристических рейсы, первый из которых длится 15 суток, второй - 20, третий - 12 суток. Вернувшись в порт, теплоходы в тот же день отправляются в новый рейс. Сегодня из порта вышли теплоходы по всем трем маршрутам. Через сколько суток они снова вместе выйдут в плавание?

4. Число m кратно 12. Докажите, что m делится на 4.

5. Найдите наибольшее двухзначность число, кратное числам 2 и 7.

6. Найдите НОД чисел: а) 12 и 24; б) 75 и 45; в) 81 и 243. Есть среди них взаимно простые?

7. Выполните действия: (1,87 + 1, 955) : 0,85 - (2 · 1,75 - 3,5) · 4,62.

V. Итог урока

Подводя итоги, следует подчеркнуть, что основное содержание темы «Делимость чисел» рассмотрены основные понятия и алгоритмы можно найти в конспектах 1-5, поэтому основная цель следующего урока - доработать темы НСД и НСК и показать понимание изученного материала и умение его применять для решения соответствующих упражнений.

VI. Домашнее задание

1. Найдите наименьшее общее кратное чисел: а) 50 и 75; б) 120 и 180; в) 370 и 740.

2. На сколько НСК (80, 100) меньше по НСК (7, 100)?

3. Какое наименьшее трицифрове число кратное числам 5 и 13?

4. Даны числа а = 23 · 52, b = 32 · 5 i c = 2 · 32. Вычислите:
а) НСК (a, b); б) НСК (а, с); в) НСК (а, b, с).

Задача. Проволока длиной 43 м разрезали на две части так, что одна из них оказалась в 3 раза длиннее второй. Найдите длину более длинной части.