УРОК № 58
Тема. Шар. Площадь поверхности и объем шара
Цель урока: повторение, приведение в систему и расширение сведений о шар (сферу), площадь поверхности и объем шара; формирование умений учащихся находить площади поверхностей и объемы шаров.
Тип урока: комбинированный.
Наглядность и оборудование: таблица «Начальные сведения стереометрии» [13]; модели пуль.
Требования к уровню подготовки учащихся: объясняют, что такое пуля и ее элементы; изображают и находят на рисунке шар; записывают и объясняют формулы площади поверхности и объема шара; применяют изученный материал к решению задач, в том числе и прикладного содержания.
Ход урока
И. Проверка домашнего задания
Проверить наличие выполненного домашнего задания и ответить на вопросы, которые возникли у учащихся при решении задачи.
Решение
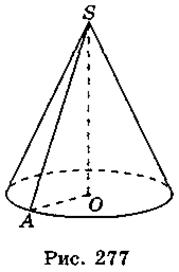
Пусть SA = 15 см, SO = 9 см (рис. 277). Из треугольника SAO имеем: АО = 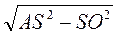 =
= 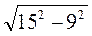 = 12 (см).
= 12 (см).
Sкон = Sосн + Sбоков = n ∙ AO2 + n ∙ AO ∙ AS = n ∙ 122 + n ∙ 12 ∙ 15 = 144n + 180n = 324n(см2). V = 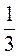 nАО2 ∙ SO =
nАО2 ∙ SO = 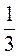 n ∙ 144 ∙ 9 = 432(см3).
n ∙ 144 ∙ 9 = 432(см3).
Ответ. 324n см2, 432n см3.
Фронтальная беседа
Конус образован в результате вращения прямоугольного треугольника вокруг катета (рис. 278), равна а и образует угол α с гипотенузой. Определите, какие из приведенных утверждений являются правильными, а какие - неправильными.
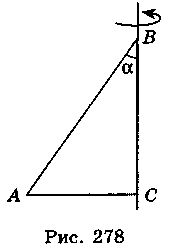
а) Образующая конуса равна acosα.
б) Радиус конуса равен 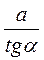 .
.
в) Площадь боковой поверхности конуса равна nа2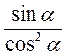 .
.
г) Объем конуса равен 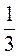 na3 tg2α.
na3 tg2α.
II. Поэтапное восприятие и осознание нового материала
Пуля и ее элементы
Шаром называется тело, образованное вращением круга вокруг диаметра (рис. 279).
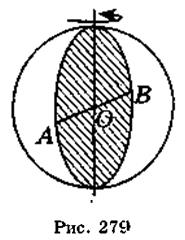
Сферой называется фигура, образованная вращением круга вокруг диаметра. (Демонстрируются модели шаров (сфер).)
Можно дать и другие определения сферы и шара.
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии (которая называется радиусом) от данной точки (которая называется центром).
Отрезок, соединяющий центр сферы с точкой сферы, называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через центр сферы, называется диаметром сферы. На рис. 279 точка О - центр сферы, ОА, ОВ - радиус сферы АВ - диаметр сферы.
Шаром называется тело, которое состоит из всех точек пространства, которые расположены от данной точки на расстоянии, не превышающей данную. Эта точка называется центром шара, а данное расстояние - радиусом шара.
Плоскость, которая проходит через центр шара (сферы), называется диаметральной плоскостью.
Сечение шара (сферы) диаметральной плоскостью называются большим кругом (большим кругом).
Задача класса
- 1. Приведите примеры бытовых предметов, имеющих форму шара (сферы).
- 2. Радиус шара
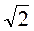 см. Укажите, внутри или вне шара размещена точка А, если она удалена:
см. Укажите, внутри или вне шара размещена точка А, если она удалена:
а) от центра шара на 1 см;
б) от центра шара на 1,5 см.
Площадь поверхности и объем шара
Строгие рассуждения (мы их не. приводим) показывают, что площадь сферы в 4 раза больше площади большого круга.
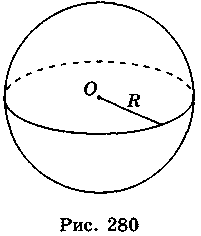
Следовательно, если радиус сферы - R (рис. 280), то его площадь: S = 4nR2.
Объем шара вычисляется по формуле V = 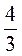 nR3.
nR3.
Решение задач
- 1. Найдите площадь поверхности шара, диаметр которого 10 см.
- 2. Площадь большого круга шара равна 20π см2. Найдите площадь поверхности шара.
- 3. Радиус шара равен 9 см. Найдите объем шара.
- 4. Найдите объем шара, диаметр которого равен 12 см.
- 5. Найдите площадь большого круга и длину большого круга, если радиус шара равен 2 см.
Приводим образец конспекта учащихся (табл. 14).
Таблица 14
Шар (сфера) |
|
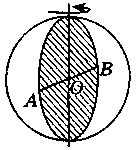
Шар (сфера) - фигура, образованная вращением круга (круга) вокруг его диаметра.
О - центр шара (сферы);
ОА, ОВ - радиусы; АВ - диаметр |
|
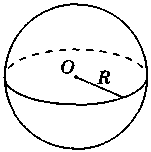
Площадь поверхности шара (площадь сферы)
S = 4nR2
Объем шара
V = 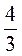 nR3 nR3 |
III. Закрепление и осмысление нового материала
Решение задач
- 1. Объемы двух шаров относятся как 27 : 64. Как относятся площади их поверхностей?
- 2. Площади поверхностей двух шаров относятся как 9 : 16. Как относятся объемы шаров?
- 3. Предположим, что Земля имеет форму шара радиусом около 6400 км, тогда суша составляет 30% площади всей поверхности планеты. Найдите площадь суши. (Ответ. 154 337 280 км2.)
- 4. Две чугунные шары диаметром 8 см и 12 см переплавили в один шар. Найдите радиус этого шара.
IV. Самостоятельная работа
Самостоятельную работу обучающего характера можно провести за пособием [14], тест 19 «Тела вращения».
V. Домашнее задание
- 1. Изучить формулы площади поверхности и объема шара.
- 2. Подготовиться к тематической контрольной работы.
- 3. Решить задачу.
- 4. Площадь сферы равна 400π см2. Найдите ее объем.
VI. Подведение итогов урока
Вопрос к классу
- 1. Дайте определение шара (сферы).
- 2. Что такое большой круг (большой круг)?
- 3. Чему равна площадь сферы?
- 4. Чему равен объем шара?