Урок 59
Тема. Угол между векторами. Скалярное произведение векторов
Цель урока: формирование понятий угла между векторами, скалярного произведения векторов. Формирование умений учащихся применять изученный материал к решению задач.
Оборудование: схема "Векторы в пространстве»
Ход урока
И. Проверка домашнего задания
1. Фронтальная беседа с классом с контрольными вопросами № 18 - 20 с использованием схемы «Векторы в пространстве» (см. стр. 233).
2. Ответы на вопросы, которые возникли у учащихся при решении задач № 51-53.
3. Математический диктант.
Даны векторы:
Вариант 1 -  (3; 0; 4);
(3; 0; 4);  (7; 0; 2);
(7; 0; 2);
Вариант 2 -  (2; -2; 0);
(2; -2; 0);  (3; 0; -3).
(3; 0; -3).
Запишите:
1) координаты вектора 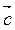 , если
, если 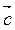 =
=  +
+  , (2 балла)
, (2 балла)
2) координаты вектора 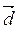 , если
, если 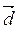 = 2
= 2 -
-  ; (2 балла)
; (2 балла)
3) длину вектора  +
+  ; (2 балла)
; (2 балла)
4) координаты вектора 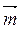 , если известно, что длина вектора
, если известно, что длина вектора 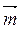 втрое больше длины вектора
втрое больше длины вектора  ; (2 балла)
; (2 балла)
5) при каком значении k вектор 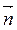 (k; 0; 6) колінеарний вектора
(k; 0; 6) колінеарний вектора  ; (2 балла)
; (2 балла)
6) компланарні векторы  ,
,  и
и 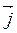 (0; 0; 1)? (2 балла)
(0; 0; 1)? (2 балла)
Ответ. Вариант 1. 1) 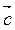 (10; 0; 6). 2)
(10; 0; 6). 2) 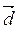 (-1; 0; 6). 3) 2
(-1; 0; 6). 3) 2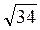 . 4)
. 4) 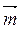 (-9; 0; -12),
(-9; 0; -12), 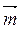 (9; 0; 12). 5) k = 21. 6) Да.
(9; 0; 12). 5) k = 21. 6) Да.
Вариант 2. 1) 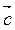 (5; -2; -3). 2)
(5; -2; -3). 2) 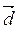 (1; -4; 3). 3)
(1; -4; 3). 3) 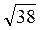 . 4)
. 4) 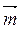 (6; -6; 0),
(6; -6; 0), 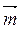 (-6; 6; 0). 5) k = - 6. 6) Hi.
(-6; 6; 0). 5) k = - 6. 6) Hi.
II. Восприятие и осознание нового материала
Скалярное произведение векторов
Скалярным произведением векторов  (аx; y; z) ∙
(аx; y; z) ∙  (bx; by; bz) называется число (скаляр)
(bx; by; bz) называется число (скаляр)  ·
·  = аx · bx + аy · by + аz · bz.
= аx · bx + аy · by + аz · bz.
Решение задач
1. Найдите  ·
·  , если
, если  (-2; 3; 1),
(-2; 3; 1),  (-4; -5; 2).
(-4; -5; 2).
2. Даны векторы  (2; -1; 4),
(2; -1; 4),  (5; 3; n). При каком значении п скалярное произведение векторов равна -3?
(5; 3; n). При каком значении п скалярное произведение векторов равна -3?
Из определения скалярного произведения двух векторов  и
и  вытекают его свойства.
вытекают его свойства.
1)  ·
·  =
=  ·
·  .
.
2) ( +
+  ) ·
) · 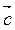 =
=  ·
· 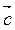 +
+  ·
· 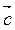 .
.
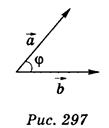
3) Скалярное произведение векторов  и
и  равно произведению их абсолютных величин на косинус угла между ними:
равно произведению их абсолютных величин на косинус угла между ними:  ·
·  =
=  ·
·  cos φ (рис. 297).
cos φ (рис. 297).
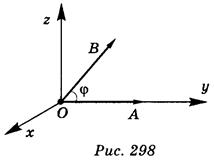
Доведение
От точки О отложим вектор O =  (рис. 298) и ОА =
(рис. 298) и ОА =  . Выберем декартову систему координат так, чтобы точка О была началом координат, прямая ОА совпала с осью у, ось z была бы перпендикулярна к прямой ОА и находилась в плоскости ОАВ, ось х перпендикулярна к плоскости вz. Определим координаты векторов
. Выберем декартову систему координат так, чтобы точка О была началом координат, прямая ОА совпала с осью у, ось z была бы перпендикулярна к прямой ОА и находилась в плоскости ОАВ, ось х перпендикулярна к плоскости вz. Определим координаты векторов  и
и  :
:
А(0; | | ; 0); B(0; |
| ; 0); B(0; | | cos φ; |
| cos φ; | | sin φ);
| sin φ);  (0; |
(0; | |; 0);
|; 0);  (0; |
(0; | | cos φ; |
| cos φ; | | sin φ).
| sin φ).
Найдем скалярное произведение:
 ·
·  = 0 · 0 + |
= 0 · 0 + | | · |
| · | | cos φ + 0 · |
| cos φ + 0 · | | sin φ = |
| sin φ = | | · |
| · | | cos φ.
| cos φ.
Следствия из свойства 3:
1) 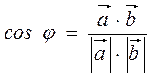
2) Две отличные от нуля векторы  и
и  перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю.
перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю.
Действительно, если  ·
·  = 0, то
= 0, то  ·
·  · cos φ = 0 , cos φ = 0, φ =
· cos φ = 0 , cos φ = 0, φ = 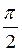 , и наоборот, если φ = 0 , то
, и наоборот, если φ = 0 , то  ·
·  =
=  ·
·  · cos φ =
· cos φ =  ·
·  · 0 = 0.
· 0 = 0.
Решение задач
1. Найдите  ·
·  , если
, если  = 5,
= 5,  = 4, а угол между векторами равен 120°.
= 4, а угол между векторами равен 120°.
2. Ребро куба равно 4 (рис. 299). Найдите 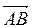 ·
· 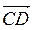 .
.
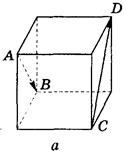
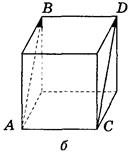
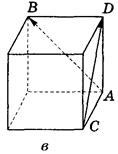
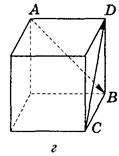
Рис. 299
3. Или перпендикулярные векторы  (2; 3; 6) и
(2; 3; 6) и  (3; 2; -1)?
(3; 2; -1)?
4. При каком значении т векторы  (6; 0; 12) и
(6; 0; 12) и  (-8; 13; m) перпендикулярны?
(-8; 13; m) перпендикулярны?
5. Есть ли среди векторов  (2; 3; 1),
(2; 3; 1),  (5; 9; 2),
(5; 9; 2), 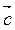 (-3, 1; 3) ортогональные векторы?
(-3, 1; 3) ортогональные векторы?
6. Какой угол образуют векторы  (-5; 0; 0) и
(-5; 0; 0) и  (0; 3; 0)?
(0; 3; 0)?
7. Найдите угол между векторами  (1; 1; 0) и
(1; 1; 0) и  (1; 0; 1).
(1; 0; 1).
8. Найдите cos ABC, если А(1; -3; 4), В(2; -2; 6), С(3; 1; 3).
III. Домашнее задание
§4, п. 35, 36; контрольные вопросы № 18-20; задачи№ 55 (1; 4), 56 (с. 58).
IV. Подведение итога урока
Вопрос к классу
1) Что называется скалярным произведением векторов  (аx; y; z) и
(аx; y; z) и  (bx; by; bz)?
(bx; by; bz)?
2) Сформулируйте свойства скалярного произведения векторов.
3) условие ортогональности двух ненулевых векторов?
4) В пространстве даны векторы  (1; 1; -1),
(1; 1; -1),  (0; -1; 1). Укажите, какие из указанных утверждений правильные, а какие - неправильные:
(0; -1; 1). Укажите, какие из указанных утверждений правильные, а какие - неправильные:
а) 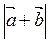 = 1;
= 1;
б) векторы  и
и  перпендикулярны;
перпендикулярны;
в) векторы  +
+  и
и  не перпендикулярны;
не перпендикулярны;
г)  ·(
·( +
+ ) = 1;
) = 1;
д) векторы  и
и  +
+  образуют угол, косинус которого равен
образуют угол, косинус которого равен 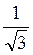 .
.