Урок 58
Тема. Векторы в пространстве (равенство векторов, коллинеарность векторов, компланарність векторов).
Сложение, вычитание векторов, умножение вектора на число, свойства действий над векторами
Цель урока: формирование знаний учащихся о векторах в пространстве, действия над векторами, заданными координатами, Формирование умений применять изученный материал к решению задач.
Оборудование: схема «Векторы в пространстве».
Ход урока
И. Проверка домашнего задания
I. Проверить правильность выполнения задачи № 63 по заготовленными
записями на доске.
Решение задачи № 63
Пусть SO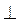 α,
α,  SAO = 45°,
SAO = 45°,  OAB = 45° (рис. 292). Проведем SO
OAB = 45° (рис. 292). Проведем SO ОА. Пусть SO = а; тогда ОА = а, OB = a. ΔOSA = ΔOSB = ΔОАВ (за двумя катетами). Из равенства треугольников следует, что SA = SB = AB, т.е. ΔSAB - равносторонний; следовательно,
ОА. Пусть SO = а; тогда ОА = а, OB = a. ΔOSA = ΔOSB = ΔОАВ (за двумя катетами). Из равенства треугольников следует, что SA = SB = AB, т.е. ΔSAB - равносторонний; следовательно,  SAB = 60°.
SAB = 60°.
Ответ. 60°.
II. Восприятие и осознание нового материала
Ученикам предлагается прочитать в учебнике п. 35 и 36 и познакомиться с векторами в пространстве и действиями над векторами в пространстве.
Далее предлагается фронтально обсуждать вопросы и выполнять дополнительные задания.
1. Что такое вектор? Что такое абсолютная величина вектора? Какие векторы называются одинаково напрямленими? противоположно напрямленими?
Задачи.
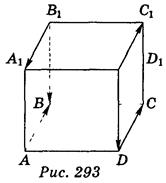
а) Укажите одинаково направлены, противоположно направленные векторы среди векторов, которые указаны на изображении прямоугольного параллелепипеда (рис. 293).
б) Найдите | |, |
|, |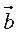 |,|
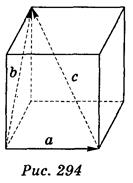
|,|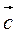 | (рис. 294), если на рисунке изображен куб с ребром 5 см.
| (рис. 294), если на рисунке изображен куб с ребром 5 см.
2. Какие векторы называются равными? противоположными?
Задачи.
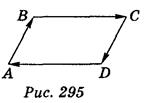
а) ABCD - параллелограмм (рис. 295). Какие векторные равенства можно записать?
б) возможно Ли равенство векторов АВ и ВА ?
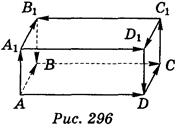
в) Укажите равные и противоположные векторы, если на рис.296 изображен прямоугольный параллелепипед.
3. Дайте определение координат вектора с началом в точке А (а1; а2; а3) и концом В точке В (b1; b2; b3). Условие равенства векторов, заданных координатами?
Задачи.
а) Даны точки А (2; 3; 4), B(1; 1; 1). Какие координаты векторов 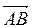 ,
, 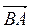 ?
?
б) координаты вектора 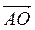 , если А (5; 1; -3), точка О - начало координат?
, если А (5; 1; -3), точка О - начало координат?
в) Когда вектор  (1; 2; 3) отложили от начала координат, то получили вектор ОА. Какие координаты точки А?
(1; 2; 3) отложили от начала координат, то получили вектор ОА. Какие координаты точки А?
г) Найти |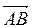 |, если А (1; 2; 3), В (3; 2; 1).
|, если А (1; 2; 3), В (3; 2; 1).
д) Даны точки А(3; -2; 5), В(-4; 6; 1), С(-2; - 6; -11), D(х; у; z). Найдите х, у, z, если 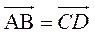 .
.
е) Абсолютная величина вектора  (5; 3; z) равна 9. Найдите z.
(5; 3; z) равна 9. Найдите z.
4. Что называется суммой (разностью) векторов  (аx; y; z) и
(аx; y; z) и 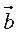 (bx; by; bz)? Условие принадлежности точек А, В, С прямой?
(bx; by; bz)? Условие принадлежности точек А, В, С прямой?
Задачи.
а) Даны векторы  (4; -5; 6),
(4; -5; 6), 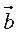 (-1; 2; 5). Найдите:
(-1; 2; 5). Найдите:  +
+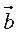 ,
,  -
- 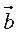 , |
, | +
+ 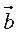 |, |
|, | -
- 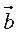 |.
|.
б) лежат Ли на одной прямой точки А, В, С, если А(3; -7; 8), В(-5; 4; 1), С (27; -40; 29)?
в) Найдите координаты точки C такой, что СА + СВ = 0, если А(-5; 7; 12), В(4; -8; 3).
г) Найдите координаты векторов  и
и  , если
, если 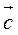 =
=  +
+ 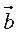 ,
, 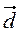 =
=  -
- 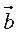 ,
, 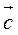 (4; -1; 5),
(4; -1; 5), 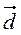 (6; 3; 1).
(6; 3; 1).
д) может быть нулевым вектором сумма трех векторов, модули которых равны 7; 1; 8?
е) Упростите: 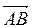 +
+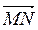 +
+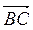 +
+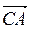 +
+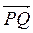 +
+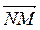 ;
; 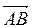 +
+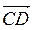 +
+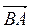 +
+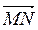 +
+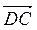 +
+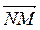 .
.
5. Что называется произведением вектора  (аx; y; z) на число λ? Какие векторы называются коллинеарными? Условие колінеарності ненулевых векторов?
(аx; y; z) на число λ? Какие векторы называются коллинеарными? Условие колінеарності ненулевых векторов?
Задачи.
а) Дано  (1; -2; 3),
(1; -2; 3), 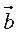 (-2; 1; -3). Найдите координаты векторов 2
(-2; 1; -3). Найдите координаты векторов 2 ; - 3
; - 3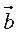 ; 2
; 2 + 3
+ 3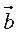 ; 2
; 2 - 3
- 3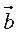 .
.
б) Найдите |2 |, если
|, если  (1; 2; 2).
(1; 2; 2).
в) коллинеарны Ли векторы  (2; 3; 8) и
(2; 3; 8) и 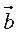 (-4; 6; - 16) ?
(-4; 6; - 16) ?
г) При каком значении т и п векторы  (15; т; 1) и
(15; т; 1) и 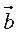 (18; 12; п) коллинеарны?
(18; 12; п) коллинеарны?
д) коллинеарны Ли векторы АВ и CD, если А(3; -2; 5), B(-1; 4; 7), C(1; 3; 6), D(-3; 9; 18)?
е) При каких значениях т и п векторы АВ и CD коллинеарны, если A(1; 0; 2), B(3; n; 5), C(2; 2; 0), D(5; 4; m)?
6. Три вектора называют компланарними, если соответствующие им направленные отрезки размещены в параллельных плоскостях. Векторы 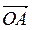 ,
, 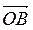 и
и 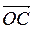 компланарні только при условии, что точки О, А, В, С лежат в одной плоскости.
компланарні только при условии, что точки О, А, В, С лежат в одной плоскости.
Задачи.
а) компланарні векторы  (3; 2; 0),
(3; 2; 0), 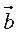 (6; 3; 0),
(6; 3; 0), 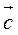 (8; 1; 0)?
(8; 1; 0)?
б) ABCD - тетраэдр, К, Р, Т - середины его ребер АВ, АС и AD. Или компланарні векторы 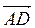 ,
, 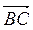 и
и 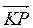 ;
; 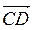 ,
, 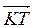 и
и 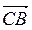 ?
?
III. Домашнее задание
§4, п. 35-36; контрольные вопросы № 18-20; задачи № 51-53 (с. 58).
IV. Подведение итога урока
Подведение итога урока целесообразно провести с использованием данной схемы.