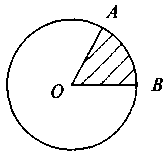Урок № 58
Тема. Круговой сектор
Цель: сформировать представление о полный угол, круговой сектор и измерения секторов частями полного угла; отработать навыки решения задач на применение формул C = nD, S = nR2 и понятие кругового сектора.
Тип урока: усвоение умений и навыков.
Ход урока
И. Проверка домашнего задания
@ Выборочно (у «слабых» учеников на перемене проверяем качество выполнения домашнего задания) на уроке фронтально проверяем выполнение домашних задач 2, 3. Усвоение формулы S = nR2 и навыков ее применения можно проверить, выполнив математический диктант.
1. Напишите формулу, по которой вычисляется площадь круга, если известен радиус окружности.
2. Округлите число n до сотых и запишите результат.
3. Вычислите площадь круга, длина радиуса которого 3 дм, округлив n до сотых.
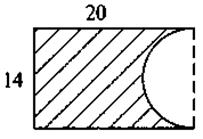
4. Вычислите площадь фигуры, изображенной на рисунке, взяв число n в виде неправильной дроби.
II. Актуализация опорных знаний
Игровой момент
Закончите предложения:
Фигура, состоящая из круга и части плоскости, которая находится внутри окружности, называется...
Отрезок, соединяющий центр окружности с точкой на окружности, называется...
Фигура, состоящая из точки и двух лучей, выходящих из этой точки, называется...
Угол измеряется в...
Наибольший из углов... Его градусная мера...
III. Формирование знаний
1. Понятие кругового сектора
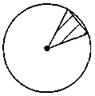
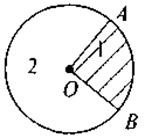
Конструктивно формируем представление о сектор: Круг с центром в т. О и радиусом О А и О В делится на две части: один и два - круговые секторы.
@ Автор считает, что не надо от учеников требовать знания определение сектора (как часть круга, ограниченная двумя радиусами), но уметь изображать и находить на готовых рисунках эти фигуры обязательно.
2. Как измеряются круговые секторы?
а) Градусной мере угла, образующие радиусы;
б) можно находить площадь сектора.
3. Чему равна сумма градусных мер всех секторов данного круга?
На рис. ОА и ОВ - радиусы, следовательно, имеем два сектора: первый и второй, но  1 = 180° и
1 = 180° и 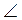 2 = 180°, поэтому
2 = 180°, поэтому 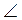 1 +
1 + 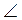 2 = 360° полный угол.
2 = 360° полный угол.
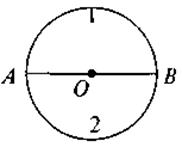
Итак, запомните, полный угол - 360°. Сколько градусов составляет круговой сектор, если он составляет  ;
; 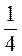 ; 5 % полного угла?
; 5 % полного угла?
Итог
1. Сектор - это фигура, которая является частью круга, ограниченная двумя радиусами круга.
2. Сектор характеризуется:
а) градусной мере угла, который образуют его радиусы; б) площадью.
IV. Применение знаний. Формирование умений
Решение упражнений
@Основная цель - научиться строить секторы, если известно, какую часть (выраженную дробью или процентами) сектор составляет от полного угла, а также не забываем выполнять задачи на применение формул C = nD i S = nR2.
Задача 1. Разделите круг на секторы, углы которых составляют 15 %; 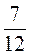 ; 0,2 полного угла соответственно. Вычислите величину угла четвертого сектора.
; 0,2 полного угла соответственно. Вычислите величину угла четвертого сектора.
Задача 2. Разделите угол на сектора, если градусная мера одного из их углов на 20° больше градусную меру второго и на 40° меньше градусной меры третьего.
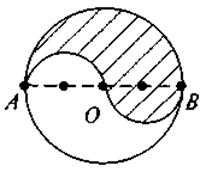
Задача 3. Дан круг с центром О и радиусом 12 см (рис). Найдите площадь заштрихованного сектора, если 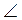 AOB = 60°.
AOB = 60°.
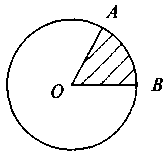
(Перед решением этой задачи можно предложить учащимся следующий вопрос:
Какую часть составляет площадь сектора от площади круга, если градусная мера круга сектора составляет: а) 90°; б) 30°; в) 45°; г) 1°?)
Задача 4. Длина диаметра круга 70 см. Сколько примерно надо сделать оборотов, чтобы преодолеть расстояние в 3 км?
Задача 5. Найдите площадь заштрихованной фигуры, выполнив необходимые вычисления:
а)
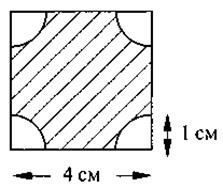 |
б) АВ = 4см
|
V. Итоги урока
Бліцтест
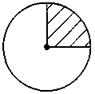
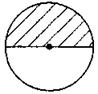
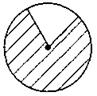
1. На каком из рисунков заштрихованная фигура не является круговым сектором?
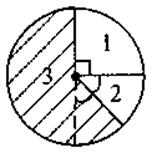
2. Найдите угол, которым измеряется сектор 3 на рисунке.
а) 180°; б) 90°; в) 225°; г) 360°.
VI. Домашнее задание
Задача 1. Начертите круг радиусом 2,5 см. Проведите радиус ОА, диаметр АВ, хорду ВС, заштрихуйте сектор АОС.
Задача 2. Длина окружности равна 12,56 дм. Найдите площадь круга, ограниченного этой окружностью.
Задача 3. Разделите круг на секторы, углы которых составляют 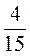 ; 0,4; 25 % полного круга соответственно. Вычислите величину угла четвертого сектора.
; 0,4; 25 % полного круга соответственно. Вычислите величину угла четвертого сектора.