Урок № 57

Тема. Преобразование целых выражений

Цель: обобщить и систематизировать знания, умения, навыки учащихся; подготовиться к тематической контрольной работы.

Тип урока: обобщение и систематизация знаний.

Ход урока

I. Организационный момент

Учитель проверяет готовность учащихся к уроку и сообщает тему.

II. Проверка домашнего задания

1. Упражнения № 1 и 2 из домашнего задания являются упражнениями на закрепление навыков, формирование которых началось на предыдущем уроке. Поэтому проверку этой части домашнего задания выполняем или выборочно (у «слабых» учеников) или побуждаем учащихся к самопроверке и отвечаем на вопросы, возникшие у учащихся при решении этих задач.

2. Работа с опережающим домашним заданием,

@ Эта часть домашнего задания является очень важной, так как является фундаментом для осуществления обобщения и систематизации и, возможно, и коррекции знаний, умений и навыков накануне тематической контрольной работы. Поэтому эту часть домашнего задания проверяем тщательно. Ученики презентуют выписаны понятия и аргументируют свой выбор.

Следующим шагом должно идти установления связей (логики) между выписанными элементами и понятиями. После обсуждения можем сделать определенные выводы.

Во время работы с целыми выражениями (а именно такие рассматриваются в 7 классе) мы осуществляем два обращены виды преобразований: а) записать выражение в виде многочлена (суммы); б) преобразовать в многочлен (сумму) в произведение (разложить на множители).

Можно выделить такие способы тождественных преобразований целого выражения в многочлен:

1) раскрытие скобок;

2) возведение подобных членов многочлена;

3) преобразования одночлен в одночлен стандартного вида;

4) сложение и вычитание многочленов;

5) умножение одночлена на многочлен и многочлена на многочлен;

6) применение формул сокращенного умножения.

Напоминаем такие способы преобразования суммы в произведение (разложения на множители):

1) вынесение общего множителя за скобки;

2) применение формул сокращенного умножения;

3) группировка и некоторые специальные приемы (перегруппировка, сведение к разности квадратов).

Основные виды задач, при решении которых используют названные преобразования:

1) вычисление значений выражений;

2) решение уравнений;

3) доведение делимости;

4) поиск наибольшего или наименьшего значения выражения.

После обсуждения составляем схему:

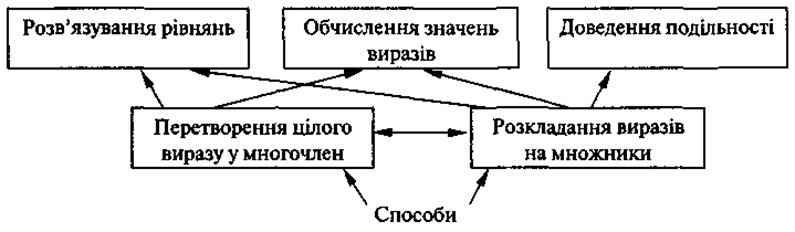
1) a + (b - c) = a + b - c

2) а - (b - с) = а - b + с

3) а(b + с) = аb + ас

4) (а ± b)2 = а2 ± 2аb + b2

5) (а - b)(а + b) = а2 - b2

6) (а ± b)(а2 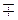аb + b2) = а3 ± b3

III. Формулировка цели и задачи урока

@ После выполненной работы по обобщению материала формулируем цель урока: 1) обобщить учебный материал по способам некоторых преобразований выражений; 2) обобщить и систематизировать умения выполнять названные преобразования и навыки применения во время решения задач.

IV. Обобщение и систематизация умений и навыков

@ Этот этап урока предусматривает обобщение усвоенных умений и навыков учащихся на конкретных типовых задачах, а также, в случае необходимости, коррекции знаний и умений учащихся. Поэтому этот этап урока желательно провести в виде работы в группах, причем группы формируются из учащихся, имеющих схожие проблемы, то есть будут обрабатывать и корректировать одни и п сами умения и навыки Для того чтобы сформировать группы, учащимся предлагается для самостоятельного выполнения тестовое задание.

1. Разложите на множители 3а2 - 3:

1) 3(а2 - 3);

2) 3(а2 - 1);

3) 3(а - 1)2;

4) 3(а - 1)(а + 1).

2. Выделите полный квадрат из выражения х2 - 14х + 50:

1) х2 + (-14x + 50);

2) (x - 7)2;

3) (х - 7)2 + 1;

4) (х - 7)2 +50.

3. Решите уравнение х3 - 6х2 - 19х = 0:

1) х = 0; 6x2 = 0; 9х = 0;

2) х(х2 - 6х + 9) = 0; х = 0 или х2 - 6х + 9 = 0;

3) х(х - 3)2 = 0; х = 0 или х - 3 = 0; 4) х3 - 6х2 = -9х.

4. Докажите, что выражение (n + 1)2 - (n - 1)2 (делится на 4):
1) (n + 1)2 - (n - 1)2 = (n + 1 - (n - 1))(n + 1 + n - 1) = 2 ∙ (2n) = 4n 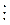4;

2) (n + 1)2 - (n - 1)2 = n2 + 1 - n2 - 1 = 0 делится на 4;

3) (n + 1)2 - (n - 1)2 = n2 + 2n + 1 - (n2 - 2n + 1) = n2 + 2n + 1 - n2 + 2n - 1 = 4n 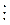4;

4) другой вариант.

После проведения и проверки тестов ученики объединяются в гомогенные группы, и следующая работа проводится в группах с последующей презентацией результатов работы.

Группа № 1. Тема. Применение различных способов разложения многочленов на множители.

Задача 1. Повторите по учебнику или тетрадью теорию: алгоритм применения различных способов разложения многочленов на множители.

Задание 2. Используя повторен алгоритм, разложите на множители:

1) х3 - 4х;

2) х4у2 - х2у4;

3) 1,44а2 - b2;

4) (с2 + 1)2 - 4с2;

5) а2 - 2аb + b2 - 1;

6) 25m2 - (4m - 4)2;

7) х2 - у2 - х - в;

8) 2a2 - 2b2 - (a - b)2;

9) a3 - 64;

10) а5 - а3 + а2 - 1.

Группа № 2. Тема. Выделение полного квадрата двучлена.

Задача 1. а) За учебником или конспектом в тетради повторить формулы квадрата двучлена и алгоритм выделения квадрата двучлена из квадратного трехчлена; б) как определить наименьшее значение выражения х2 + а?

Задача 2. а) Представьте в виде квадрата двучлена х2 + 8х + 16;

б) выделите квадрат двучлена из выражения х2 + 8х + 18;

в) каких значений приобретает выражение, полученный в п. б)? Какое значение является наименьшим? При каком значении переменной выражение приобретает значение этого?

Группа № 3. Тема. Решение уравнений с применением различных способов, пошагового преобразования выражений.

Задача 1. За конспектом, справочником или учебником повторите: 1) как свести решение уравнения к решению линейного уравнения с одной переменной; 2) как решить уравнение, если левая часть его является произведением двух или более линейных множителей, а правая часть является нулем; 3) какое свойство использовать, чтобы решить уравнение, если левая часть является суммой двух неотрицательных слагаемых, а правая - нуль.

Задание 2. Решите уравнение и прокомментируйте ход решения.

1) x2 - 9х = 0;

2) в(у2 + 3) = 4у;

3) х3 - 5х2 - х + 5 = 0;

4*) (х2 - 1)2 + (х2 - х)2 = 0.

Группа № 4. Тема. Доказательства делимости.

Задача 1.1) Какое число называют делителем данного числа?

2) Как доказать, что выражение А делится на данное число?

Задание 2. Докажите, что:

1) при любом целом значении п значение выражения (2n + 7)(8n - 8) - (4n + 5)2 не делится на 6;

2) значение выражения делится на данное число:

а) 4012 - 1992 на 600;

б) 583 + 423 на 100;

в) 825 - 6412 на 7;

г) 169 - 328 + 812 на 7;

д*) разность квадратов двух целых чисел, которые не делятся на 3, кратна 3.

V. Итоги урока

@ Опять возвращаемся к схеме, составленной в начале урока, и повторяем основные теоретические моменты и способы действий.

VI. Домашнее задание

Домашняя контрольная работа

№ 1. Упростите выражение:

1) (а - 6)(а + 6) + (3 - а)2 - (2а + 1)2 - (а - 3)(а + 4);

2) (а2 - b2)(а2 + b2)(а4 + b4) + а8 + b8.

№ 2. Разложите на множители:

1) 9у2 - 16;

2) 3х2 - 3у2;

3) 27а3 - b3;

4) b6 - 4b4;

5) 0,8а3 + 0,4а2 + 0,4а4;

6) m3 - n3 + 3m2 + 3mn + 3n2;

7) а2 + b2 + с2 - х2 + 2аb + 2bс + 2са.

№ 3. Решите уравнение:

1) (х2 - 1)(х2 + 1)(x4 + 1) = x8 + 4x;

2) х2 - 9 = х - 9х2.

№ 4. Докажите, что:

1) выражение х2 + 10х - 27 приобретает лишь отрицательных значений;

2) если число n от деления на 5 дает остаток 3, а число m - остаток 4; число n2 + m2 делится на 5.