Урок 57
Тема. Решение задач на нахождение углов в пространстве
Цель урока: формирование умений учащихся находить углы в пространстве.
Оборудование: стереометрический набор, модель куба.
Ход урока
И. Проверка домашнего задания
1. Два ученика воспроизводят решения задач № 48 (2) 49 (1) на доске.
2. Фронтальное опрашивание.
1) Сформулируйте теорему о площади ортогональной проекции многоугольника.
2) Найдите площадь ортогональной проекции квадрата с диагональю 4 см, если угол между плоскостью квадрата и его проекцией равен: а) 60°; б) 45°.
3) Ребро куба ABCDA1B1C1D1 равна 2 см. Укажите, какие из приведенных утверждений правильные, а какие - неправильные:
а) угол между прямой C1D и плоскостью АВС равен 30°;
б) угол между прямой B1D и плоскостью АВС равен 45°;
в) плоскость АСВ1 образует с плоскостью АВС угол, тангенс которого равен 
;
г) площадь сечения куба плоскостью, проходящей через ребро АВ и образует с плоскостью АВС угол 30° , равна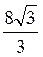 
см2.
3. Проверка правильности решения задач№ 48 (2), 49 (1), что воссоздали ученики на доске.
4. Самостоятельная работа.
Вариант 1
1) Угол между плоскостями α и β равен 60°. Точка А, лежащая в плоскости α, удаленная от плоскости β на 12 см. Найдите расстояние от точки А до линии пересечения плоскостей. (4 балла)
2) Через центр О квадрата ABCD проведен к его плоскости перпендикуляр SO. Угол между прямой SC и плоскостью квадрата равен 60°. АВ = 18 см. Найдите угол между плоскостями ASC и DSC. (8 баллов)
Вариант 2
1) Угол между плоскостями α и β равен 60°. Точка А, лежащая в плоскости α, удаленная от плоскости β на 12 см. Найдите расстояние от проекции точки А на плоскость β к линии пересечения плоскостей. (4 балла)
2) Через вершину D тупого угла ромба ABCD проведен к его плоскости перпендикуляр DM длиной 9,6 см. Диагонали ромба равны 12 и 16 см. Найдите угол между плоскостями АВС и МВД. (8 баллов)
Вариант 3
1) Угол между плоскостями α и β равен 30°. Точка А, лежащая в плоскости α, удаленная от линии пересечения плоскостей на 12 см. Найдите расстояние от точки А до плоскости β. (4 балла)
2) Через центр О квадрата ABCD проведен к его плоскости перпендикуляр SO. Угол между прямой SC и плоскостью квадрата равен 60°, АВ = 18 см. Найдите угол между плоскостями АВС и BSC. (8 баллов)
Вариант 4
1) Угол между плоскостями α и β равен 30°. Точка А, лежащая в плоскости α, удаленная от линии пересечения плоскостей на 12 см. Найдите расстояние от проекции точки А на плоскость β к линии пересечения плоскостей. (4 балла)
2) Через вершину D тупого угла ромба ABCD проведен к его плоскости перпендикуляр DM. Диагонали ромба равны 12 и 16 см. Найдите угол между плоскостями AMD и CDM. (8 баллов)
Ответ. Вариант 1. 1) 8
см. 2) arctg 
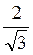. Вариант 2. 1) 4 см. 2) 45°. Вариант 3. 1) 6 см. 2) arctg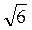 
. Вариант 4.1) 6 см. 2) n - arccos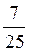 
.
II. Закрепление и осмысление знаний учащихся
Формирование умений учащихся находить углы между прямой и плоскостью, между плоскостями
Решение задач
1. Угол между прямой а и плоскостью α равен 45°. Через точку их пересечения в плоскости α проведена прямая b. Угол между прямыми а и b равен 60°. Докажите, что угол между прямой b и проекцией прямой а на плоскость α равен 45°.
2. Через сторону AC равностороннего треугольника АВС проведена плоскость α. Угол между высотой BD треугольника и данной плоскостью равен φ. Найдите угол между прямой АВ и плоскостью α. (Ответ, arcsin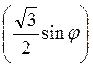 
)
3. Через центр О правильного треугольника АВС проведен к его плоскости перпендикуляр МО. АВ = а. Угол между прямой МА и плоскостью треугольника равен 45°. Найдите угол между плоскостями: 1) АМО и ВМО; 2) ВМС и АВС.
(Ответ. 1) 60°; 2) arctg 2)
4. Плоскости равносторонних треугольников АВС и ABD перпендикулярны. Найдите угол: 1) между прямой DC и плоскостью АВС; 2) между плоскостями ADC и BDC.
(Ответ. 1) 45°; 2) arccos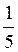
)
III. Домашнее задание
Повторить раздел «Векторы» из планиметрии и решить задачу № 63 (с. 59).
IV. Подведение итога урока
Вопрос к классу
1) Дайте определение угла между скрещивающимися прямыми.
2) Дайте определение угла между прямой и плоскостью.
3) Дайте определение угла между плоскостями.