Урок № 58

Тема. Уравнения, сводящиеся к квадратным

Цель: усвоение учащимися основных видов целых уравнений, решение которых сводится к решению квадратных уравнений и схем их решения; сформировать умение выделять изученные виды уравнений среди других уравнений, а также использовать известные схемы для решения названных видов уравнений.

Тип урока: усвоение знаний и умений.

Наглядность и оборудование: опорный конспект «Уравнения, сводящиеся к квадратным».

Ход урока

I. Организационный состояние

II. Проверка домашнего задания

Поскольку задача домашней работы были такого же типа, как и упражнения классной работы, то во время проверки уделяем внимание лишь задачей повышенной сложности (традиционно это задача на разложение выражений высших степеней на множители, в решении которых используется прием замены переменных).

III. Формулировка цели и задач урока

Учитель еще раз напоминает учащимся о том, что умение решать квадратные уравнения является одним из важнейших для дальнейшего изучения не только алгебры, но и многих смежных дисциплин. Так, тема целиком посвящена изучению вопроса о сфере применения приобретенных умений при решении задач, предусмотренных программой по математике в 8 классе.

На этом уроке будет изучен вопрос о применении умений решать квадратные уравнения в решении некоторых других видов уравнений.

IV. Актуализация опорных знаний и умений

@ С целью успешного восприятия учащимися учебного материала урока следует активизировать такие знания и умения: применять основные понятия, связанные с понятием уравнения с одной переменной; выполнение арифметических действий с действительными числами; алгоритм решения простейших дробно-рациональных уравнений; применение различных способов решения квадратных уравнений различных видов.

Выполнение устных упражнений

1. Сократите дроби: ; ; ; ; ; .

2. Найдите корни уравнений: х2 - 64 = 0; у2 + 49 = 0; 2р2 - 7р = 0; т2 = 0; 2х2 + 4х - 1 = 0; х2 + 3х + 4 = 0.

3. При каких значениях переменной х выражение 3х - 1 приобретает значений: 0; -2; 3; ?

4. Выполните умножение: (x + 1)(x - 1); (x + 1)(x - 3); (x + 1)(x + 2); (x - 1)(x - 4).

V. Усвоение знаний

План изучения нового материала

1. Примеры уравнений, сводящиеся к квадратным, путем введения новой переменной (заменой переменных). Как решать такие уравнения?

2. Какое уравнение называют біквадратним уравнением? Как решить біквадратне уравнения?

3. *Как решить уравнение вида (х + а)(х + b)(х + с)(х + d) = A, где a + d = b + c?

@ Программой по математике в разделе «Уравнения, сводящиеся к квадратным» предусмотрено изучение способов решения целых уравнений, сводящиеся к квадратным, путем введения новой переменной, а также дробно-рациональных уравнений.

На уроке проводится ознакомление учащихся с общей схемой решения уравнений, превращаются в квадратные путем введения новой переменной. Если на предыдущем уроке учащиеся хорошо усвоили прием перехода к новой переменной в ходе разложения выражений на множители, то на этом уроке у учащихся не должно быть проблем с пониманием схемы решения уравнений путем введения новой переменной - схема решения уравнений таким методом почти совпадает со схемой преобразования выражений (добавляется один пункт - после выполнения обратной замены решить добытое уравнения).

Что касается біквадратних уравнений, то их можно рассматривать как особый случай уравнений, которые были рассмотрены выше, поэтому следует заметить, что составлена выше схема используется и при решении этих уравнений (можно отметить, что, в отличие от других подобных уравнений, в біквадратних уравнениях всегда «срабатывает» замена х2 = t).

Если учащиеся имеют высокий уровень учебных достижений, их можно ознакомить со способом преобразования уравнений вида (х + a)(х + b)(х + с)(х + d) = А, где a + d = b + c, к уравнениям вида аР2(х) + bР(х) + с = 0, где Р(х) - многочлен от одной переменной, с тем, чтобы потом решить образованное уравнения рассмотренным выше способом.

VI. Формирование умений

Выполнение устных упражнений

1. Какую замену следует выполнить в уравнении, чтобы получить квадратное уравнение:
а) (х2 + 6х + 9) - 2(х + 3) - 3 = 0;

б) (х2 + 6х + 9)2 - 2(х + 3)2 - 3 = 0;

в) (х2 + 6х)2 - 2(х2 + 6х) - 3 = 0.

2. Какие квадратные уравнения получим в задаче 1, если выполним соответствующую замену?

Выполнение письменных упражнений

Для реализации дидактической мсти урока следует решить задачи следующего содержания:

1. Решение уравнений различного вида, сводящиеся к квадратным введением новой переменной. Решите уравнение:

а) (х2 - 1)2 - 11(х2 - 1) + 24 = 0;

б) (х2 + 2х)2 - 2(х2 + 2х) - 3 = 0.

2. Решения біквадратних уравнений.

Решите уравнения: а) 2х4 - 9х2 + 4 = 0; б) 36х4 - 7х2 - 4 = 0.

3. Логические упражнения и задачи повышенного уровня сложности для учащихся, имеющих достаточный и высокий уровни знаний.

1) Решите уравнение:

а) (х2 + 5х)(х2 + 5х - 2) = 24;

б) (2х2 + х + 1)(2х2 + х + 3) = 8;

в) (х2 - 5х + 7)2 - (х - 2)(х - 3) = 1;

г) (х - 1)(х - 2)(х - 3)(х - 4) = 120;

д) (x - 1)x(x + 1)(x + 2) = 24;

e) (х + 3)2(х + 2)(х + 4) = 12.

2) Решите уравнение: а) ; б) .

3) Решите уравнение: а) х - 6 + 5 = 0; б) х + - 6 = 0; в) ; г) ; д) ; е) .

4) Найдите пропущенный выражение:

4. На повторение: задачи на преобразование рациональных выражений; на решение дробных уравнений (такого уровня сложности, как было решено в теме «Рациональные выражения»).

@ В ходе решения письменных упражнений на отработку умений применять схему, предусматривающую введение новой переменной для перехода от данного уравнения к квадратному, следует требовать от учеников учета нескольких важных моментов:

· если вводить замену то только эффективную (чтобы в результате перехода к новой переменной уравнения с неквадратного превратилось в квадратное);

· решать новообразованное квадратное уравнение относительно переменной (типичная ошибка учащихся - выполнение подобных записей: t2 + 4t + 3 = 0, х1 = -1, х2 = -3);

· обязательным этапом решения уравнения путем введения новой переменной является выполнение обратной замены (конечно, в случае, когда уравнения, добытое после замены, имеет корни).

Упражнения на повторение являются подготовительными к восприятию материала следующего урока.

VII. Итоги урока

В каком случае правильно выполнено записи?

а) х4 - 3х2 + 2 = 0. Замена: х2 = t, х4 = t2, тогда t2 - 3t + 2 = 0; x1 = 1, х2 = 2.

Ответ. 1; 2.

б) х4 - 3х2 + 2 = 0. Замена: х2 = t, х4 = t2, тогда t2 - 3t + 2 = 0, t1 = 1, t2 = 2.

Обратная замена: х2 = 1 или х2 = 2, имеем: х1 = 1, х2 = .

Ответ. 1; .

в) х4 - 3х2 + 2 = 0. Замена: х2 = t (t ≥ 0), тогда t2 - 3t + 2 = 0; t1 = 1, t2 = 2;

обратная замена: х2 = 1 или х2 = 2, имеем: х = ±1, х = .

Ответ. ±1; .

VIII. Домашнее задание

1. Изучить схемы решения уравнений, сводящихся к квадратным введением новой переменной.

2. Решить упражнения на применение изученной схемы.

3. На повторение: задачи на преобразование рациональных выражений; на решение дробных уравнений (такого уровня сложности, как было решено во время изучения темы «Рациональные выражения»).
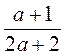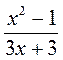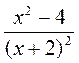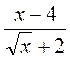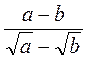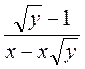