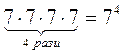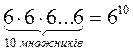УРОК 57

Тема. Квадрат и куб числа

Цель: ознакомить учащихся с понятием степени числа с натуральным показателем и терминологией (основание степени, показатель степени, степень); научить записывать произведение равных множителей в виде степени и наоборот, а также находить значения выражений, содержащих степень.

Тип урока: усвоение новых знаний.

Оборудование: таблица «Степень с натуральным показателем».

Ход урока

I. Актуализация опорных знаний

Устные упражнения

1. Запишите в виде произведения сумму:

1) 7 + 7 + 7 + 7;

2) 3 + 3 + 3 + 3 + 3;

3) а + а + а + а + а + а.

2. Найдите остаток от деления 27 514 на: 1) 10; 2) 100; 3) 1 000.

3. Найдите произведение:

1) пяти множителей, каждый из которых равен 2;

2) десяти множителей, каждый из которых равен 1;

3) трех множителей, каждый из которых равен 3;

4) двух множителей, каждый из которых равен 5;

5) тридцати множителей, каждый из которых равен 0;

6) шести множителей, каждый из которых равен 10.

II. Усвоение новых знаний

@ Преподавания нового материала можно вести традиционно по тексту учебника, а можно попробовать поставить перед учениками задачи, что приведет их к «открытию» понятия степени и понимание сути записи произведения одинаковых множителей в виде степени.

Задача 1

Запись пропущено?

Ученики сами могут установить, что выражения в левом столбце будут равняться произведению одних из равных слагаемых на их количество в сумме, и заметить похожую закономерность в коротком записи произведения одинаковых множителей в виде а^b, где а - один из одинаковых множителей, a b- число таких множителей в произведении.

После этого учитель дает определение степени некоторого числа а с натуральным показателем п, называет основные термины, связанные с понятием степень (основание, показатель степени, степень, возведение в степень), основными свойствами степени (а¹ = а; 1^п = 1; 0^п = 0), дает название втором и третьем степени числа а (а² - квадрат числа а, b³ - куб числа b) и формулирует правило выполнения действий в выражении, содержащем степень (учащиеся делают краткие записи в тетрадях схемы «Степень с натуральным показателем»).

Степень с натуральным показателем

III. Закрепление материала

На закрепление терминологии можно предложить устно:

1. Назовите основание и показатель степени: 1) 4⁸; 2) 13¹⁰; 3) ⁹; 4) 2³⁹; 5) 93¹.

2. Из записей неправильный? Почему?

1) 9 · 9 = 2⁹; 2) 10 · 10 · 10 = 10³; 3) b · b = b²;

4) ; 5) 5 · 6 · 6 · 6 = 6⁴.

3. Прочитайте выражение и найдите его значение:

1) 3¹; 2) 1¹⁰; 3) 0²⁵; 4) 5²; 5) 2³; 6) 3⁴.

4. Чему равны:

1) квадраты одноцифрових натуральных чисел;

2) углы натуральных чисел, меньших 4?

@ После этого следует предложить ученикам письменно выполнить упражнения:

№ 565, 567 - на вычисление значений выражений, содержащих степень. Желательно сначала учителю прочитать выражения с помощью слов «сумма», «разность», «произведение», «частика», «квадрат», «куб» числа, а потом уже требовать от учеников (это подготовит их к исполнение №№ 571, 572).

№ 579. Повторить, что запись, названный степени, состоит из двух чисел - основания и показателя. Поэтому в этом задании, поскольку значение степени есть, основа известна, единственное, что надо найти,- это показатель степени, то есть число, которое показывает, сколько одинаковых слагаемых надо перемножить, чтобы получить данное число.

№ 571. Направлен на предупреждение ошибок в установлении порядка выполнения действий в выражениях, содержащих степень.

Дополнительно: № 573 (1,2).

IV. Итог урока

Тестовые вопросы класса

1. Как называется запись 5⁴?

2. Как называется число 5 в этой записи? Что оно показывает?

3. Как называется число 4 в этой записи? Что оно показывает?

4. Как преподнести 5 в четвертой степени?

5. Правильно выполненные действия в примере 5 · 2² = 10² = 100? Почему? Какой ответ правильный?

V. Домашнее задание

п. 19, №№ 561; 564; 566; 572, повторение № 573 (3).