Урок 56

Тема. Площадь ортогональной проекции многоугольника

Цель урока: изучение теоремы о площади ортогональной проекции многоугольника, формирование умений учащихся применять изученную теорему к решению задач.

Оборудование: стереометрический набор, модель куба.

Ход урока

И. Проверка домашнего задания

1. Два ученика воспроизводят решения задач № 42, 45 на доске.

2. Фронтальное опрашивание.

1) Дайте определение угла между двумя плоскостями, которые пересекаются.

2) Чему равен угол между:

а) параллельными плоскостями;

б) перпендикулярными плоскостями?

3) В каких пределах может изменяться угол между двумя плоскостями?

4) верно Ли, что плоскость, которая пересекает параллельные плоскости, пересекает их под одинаковыми углами?

5) верно Ли, что плоскость, которая пересекает перпендикулярные плоскости, пересекает их под одинаковыми углами?

3. Проверка правильности решения задач № 42, 45, которое воссоздали ученики на доске.

II. Восприятие и осознание нового материала

Учащимся предлагается самостоятельно прочитать в учебнике доказательство теоремы 4.1 из п. 34, а затем вызываются к доске ученики, которые воспроизводят доказательство теоремы.

Задание ученикам

1. Докажите, что площадь проекции треугольника, у которого одна сторона находится в плоскости проекции, равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции.

2. Докажите теорему для случая, когда решеточным есть треугольник, у которого одна сторона параллельна плоскости проекций.

3. Докажите теорему для случая, когда решеточным есть треугольник, у которого ни одна из сторон не параллельна плоскости проекций.

4. Докажите теорему для любого многоугольника.

Решение задач

1. Найти площадь ортогональной проекции многоугольника, площадь которого равна 50 см2, а угол между плоскостью многоугольника и его проекции - 60°.

2. Найти площадь многоугольника, если площадь ортогональной проекции этого многоугольника равна 50 см2, а угол между плоскостью многоугольника и его проекцией равен 45°.

3. Площадь многоугольника равна 64 см2, а площадь ортогональной проекции - 32 см2. Найдите угол между плоскостями многоугольника и его проекции.

4. Или может площадь ортогональной проекции многоугольника равна площади этого многоугольника?

5. Ребро куба равно а. Найти площадь сечения куба плоскостью, проходящей через вершину основания под углом 30° к этой основы и пересекает все боковые ребра. (Ответ. )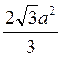

6. Задача № 48 (1, 3) из учебника (с. 58).

7. Задача № 49 (2) из учебника (с. 58).

8. Стороны прямоугольника равны 20 и 25 см. Его проекция на плоскость подобна ему. Найти периметр проекции. (Ответ. 72 см или 90 см.)

III. Домашнее задание

§4, п. 34; контрольный вопрос № 17; задачи№ 48 (2), 49 (1) (с. 58).

IV. Подведение итога урока

Вопрос к классу

1) Сформулируйте теорему о площади ортогональной проекции многоугольника.

2) может Ли площадь ортогональной проекции многоугольника быть большей площади многоугольника?

3) Через гипотенузу АВ прямоугольного треугольника АВС проведена плоскость α под углом 45° к плоскости треугольника и перпендикуляр CO до плоскости α. АС = 3 см, ВС = 4 см. Укажите, какие из приведенных утверждений правильные, а какие - неправильные:

а) угол между плоскостями АВС и α равен углу СМО, где точка Н - основание высоты СМ треугольника АВС;

б) СО = 2,4 см;

в) треугольник АОС является ортогональной проекцией треугольника АВС на плоскость α;

г) площадь треугольника АОВ равна 3 см2.

(Ответ. а) Правильное; б) неправильно; в) неправильное; г) правильное.)