УРОК № 57

Тема. Сумма первых n членов геометрической прогрессии

Цель урока: закрепить знания учащихся о содержании определения и сопутствующих понятий геометрической прогрессии, а также о ее основных свойства. Дополнить эти знания знанием формулы n-го члена геометрической прогрессии.

Закрепить умения: выделять геометрическую прогрессию среди числовых последовательностей, находить знаменатель геометрической прогрессии, первые члены геометрической прогрессии, а также использовать свойства геометрической прогрессии. Сформировать умение записывать формулу n-го члена геометрической прогрессии, а также решать различные по содержанию задачи на применение этой формулы.

Тип урока: дополнение и закрепление знаний, отработка умений и навыков.

Наглядность и оборудование: опорный конспект № 35.

Ход урока

И. Организационный этап

Учитель проверяет готовность учащихся к уроку, настраивает их на работу.

II. Проверка домашнего задания

Поскольку упражнения домашнего задания по содержанию, способу решения, а также уровню сложности соответствуют упражнениям, развязанным на предыдущем уроке, то тщательной проверке подлежат только письменные работы учащихся, требующих дополнительного педагогического внимания (эти ученики во время фронтальной работы могут выполнять индивидуальные задания соответствующего уровня сложности).

Фронтально ученики могут выполнить тестовые задания [9, тест 21], продемонстрировав уровень владения основными вопросами темы «Геометрическая прогрессия».

III. Формулировка цели и задач урока.

Мотивация учебной деятельности учащихся

Возможные ошибки при выполнении тестовых заданий на предыдущем этапе урока должны убедить учащихся в необходимости дальнейшей проработки материала предыдущего и других уроков в направлении закрепления знаний и выработки устойчивых умений использовать эти знания как в стандартных, так и в нестандартных ситуациях. Это утверждение выражает основную цель урока.

IV. Актуализация опорных знаний и умений учащихся

Устные упражнения

1. Какая последовательность называется геометрической прогрессией? Приведите пример.

2. Чему равно отношение двух соседних членов геометрической прогрессии, начиная со второго?

3. Как задать геометрическую прогрессию?

4. Как записывается формула п-го члена геометрической прогрессии?

5. Как записывается формула суммы первых л членов геометрической прогрессии, если известны:

1) ее первый член и знаменатель;

2) ее первый член, знаменатель и n-й член?

V. Отработка умений

Письменные упражнения

Содержание письменных упражнений урока может быть таким:

1) задачи на отыскание суммы последовательных членов геометрической прогрессии с n-го по m-й включительно (n m) и задачи, сводящиеся к этому;

2) задачи на применение изученных формул для отыскания неизвестных первого члена, или знаменателю, или числа n членов геометрической прогрессии с известным по условию суммой ее первых членов;

3) прикладные задачи на применение изученных на предыдущих четырех уроках формулы для геометрической прогрессии;

4) на повторение: задачи на применение формул для арифметической прогрессии.

VI. Итоги урока

Учащиеся обобщают основные типы задач на применение формул для вычисления суммы первых n членов геометрической прогрессии.

VII. Домашнее задание

1. Повторить содержание материала с опорными конспектами № 33-35.

2. Выполнить самостоятельную работу (см. ниже) с вариантом, указанным учителем.

Самостоятельная работа

Вариант 1

Найдите сумму:

1) первых пяти членов геометрической прогрессии (bn), если b1 = 8, q = ;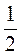

2) первых шести членов геометрической прогрессии (bn): ; ; ; ... ;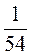

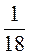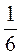3) первых семи членов геометрической прогрессии (bn), если она задана формулой общего члена bn = 3 ∙ 2n+1;

4) первых пяти членов геометрической прогрессии (bn), если сумма второго и третьего ее членов равна -12, а разность четвертого и второго членов равна 48.

Вариант 2

Найдите сумму:

1) первых пяти членов геометрической прогрессии (bn), если b1 = 625, q = 0,2;

2) первых шести членов геометрической прогрессии (bn): 18; 24; 32; ...;

3) первых пяти членов геометрической прогрессии (bn), если она задана формулой общего члена bn = 5 ∙ 2n-1;

4) первых пяти членов геометрической прогрессии (bn), если разность третьего и второго членов равна 6, а разность четвертого и второго членов равна 30.