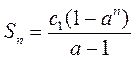УРОК № 56
Тема. Сумма первых n членов геометрической прогрессии
Цель урока: добиться усвоения учащимися формул для вычисления суммы первых п членов геометрической прогрессии. Закрепить изученные определения, свойства и формулы для геометрической прогрессии.
Выработать умения: записывать изученные формулы в соответствии с условиями задач и использовать эти записи для решения задач.
Тип урока: усвоение знаний, выработка умений.
Наглядность и оборудование: опорный конспект № 35, раздаточный материал (карточки с решениями домашней самостоятельной работы).
Ход урока
I. Организационный этап
Учитель проверяет готовность учащихся к уроку, настраивает их на работу.
II. Проверка домашнего задания
Учитель собирает тетради учеников на проверку и оценивает выполненную домашнюю самостоятельную работу. Для осуществления обратной связи учащимся раздаются листы с правильными развязками (учащиеся прорабатывают их самостоятельно дома и фиксируют возможные вопросы для того, чтобы задать их на следующем уроке).
III. Формулировка цели и задач урока.
Мотивация учебной деятельности учащихся
Поскольку между арифметической и геометрической прогрессиями существует достаточно большое количество схожих моментов, то и изучение основных программных вопросов, касающихся каждой из этих прогрессий, проводится по той же схеме. Поэтому так же, как это делалось на соответствующем этапе урока по теме «Сумма первых п членов арифметической прогрессии», на данном уроке можно предложить ученикам рассмотреть и обсудить одну из прикладных задач на вычисление суммы первых п членов геометрической прогрессии (например классическую задачу об изобретателе шахмат).
После составления математической модели задачи ученики осознают существование проблемы быстрого вычисления такой суммы (имеем мотивацию к учебной деятельности), а потому можем сформулировать цель урока: вывести формулы для вычисления суммы первых п членов геометрической прогрессии, а также изучить вопрос о сфере их применения.
IV. Актуализация опорных знаний и умений учащихся
Устные упражнения
1. Является ли геометрической прогрессией последовательность (хп):
1) -5; -5; -5; -5;
2) -5; 5; -5; 5;
3) 1; 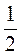 ;
; 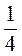 ;
; 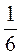 ;
; 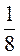 ?
?
2. Геометрическая прогрессия задана формулой n-го члена bn = 2 ∙ 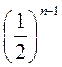 . Назовите:
. Назовите:
1) b1; 2) q; 3) b2; 4) b5.
3. Дана геометрическая прогрессия (bn). Найдите b3, если:
1) b2 = 0,2, b4 = 5;
2) b4 = 7, q = -0,1;
3) b6 = 1, b5 = 2.
V. Формирование знаний
План изучения нового материала
1. Формула для вычисления суммы первых n членов геометрической прогрессии через n-й член.
2. Формула для вычисления суммы первых n членов геометрической прогрессии через первый член и знаменатель геометрической прогрессии.
3. Примеры решения задач на применение изученных формул.
Опорный конспект № 35
Формулы суммы первых n членов геометрической прогрессии |
Если (bn) - геометрическая прогрессия, q - ее знаменатель, a Sn - сумма первых п членов, то:
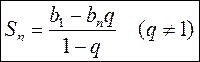 (1) (1)
или 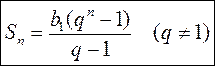 (2) (2)
! Замечание: если q = 1, то Sn = b1 ∙ n (b1 = b2 =... = bn). |
Пример 1. Найдем сумму первых восьми членов геометрической прогрессии (bn): 3; -6; 12; ... .
Решение
Имеем b1 = 3, q = 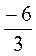 = -2, тогда по формуле (2): = -2, тогда по формуле (2):
S8 = 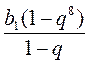 = = 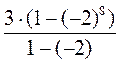 = = 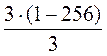 = -255. = -255.
Ответ: -255. |
Пример 2. Найдем первый член геометрической прогрессии (bn), если ее четвертый член в три раза больше третьей, а сумма первых пяти членов равна -12,1.
Решение
Поскольку b4 = 3b3, то q = 3. По условию S5 = -12,1, поэтому, поскольку 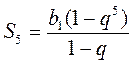 , то есть , то есть  ; -12,1 = 121b1; b1 = -0,1. ; -12,1 = 121b1; b1 = -0,1.
Ответ: -0,1. |
Методический комментарий
Вывод формул для вычисления суммы первых n членов геометрической прогрессии проводится по традиционной схеме: сначала выводится формула 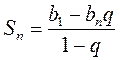 , а затем, применив к этой формулы формулу n-го члена геометрической прогрессии, выводят формулу
, а затем, применив к этой формулы формулу n-го члена геометрической прогрессии, выводят формулу 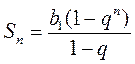 (q
(q 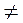 1). Так же, как и при изучении вопроса о вычисления суммы первых п членов арифметической прогрессии, после вывода формул рассматриваются наиболее типичные задачи на применение этих формул (см. опорный конспект № 35).
1). Так же, как и при изучении вопроса о вычисления суммы первых п членов арифметической прогрессии, после вывода формул рассматриваются наиболее типичные задачи на применение этих формул (см. опорный конспект № 35).
VI. Формирование умений
Письменные упражнения
Для реализации дидактической цели урока следует решить упражнения такого содержания:
1) по одной из изученных формул найти (вычислить) сумму первых п членов геометрической прогрессии;
2) решить задачи, предусматривающие прямое применение изученных формул (в условии задач напрямую не сказано, что искомая сумма является суммой геометрической прогрессии);
3) задачи на применение изученных формул для отыскания неизвестных первого члена, или разницы или числа n членов геометрической прогрессии с известным по условию суммой ее первых членов;
4) на повторение: задачи на применение изученных свойств и формул арифметической и геометрической прогрессий;
5) на повторение: упражнения на решение систем рациональных уравнений.
Методический комментарий
Предложенный набор упражнений направлен на закрепление полученной на предыдущем этапе урока формул для вычисления суммы первых п членов геометрической прогрессии, на выработку оперативных умений по их применению в стандартных ситуациях как в прямом, так и в обратном направлении, а также способствуют повторению и закреплению изученного в этой теме материала.
VII. Итоги урока
Контрольное задание
Дано геометрическую прогрессию (сn). Определите, являются ли правильными формулы, и исправьте найденные ошибки.
1) cn = cn-1 + d (d = const);
2) cn = cn-1 ∙ a (a = const, a 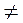 0);
0);
3) 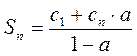 (a = const, a
(a = const, a 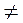 0);
0);
4) 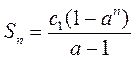 (a = const)?
(a = const)?
VIII. Домашнее задание
1. Изучить формулы для вычисления суммы первых п членов геометрической прогрессии (см. опорный конспект № 35).
2. Решить упражнения, аналогичные по содержанию и уровню сложности выполненной на уроке.
3. Повторить схему решения задач составлением математической модели.
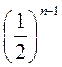
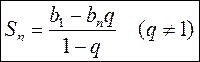
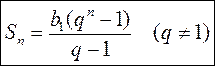
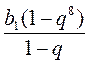 =
= 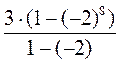 =
= 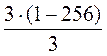
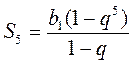

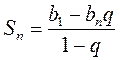
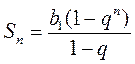
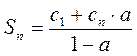 (a = const, a
(a = const, a