УРОК 57

Тема. Логарифмические уравнения

Цель урока. Формирование умений учащихся решать логарифмические уравнения.

И. Проверка домашнего задания

1. Фронтальная беседа по № 15-25 с «Вопросы и задания для повторения» раздела V и ответы на вопросы, которые возникли у учащихся в процессе выполнения домашних заданий.

2. Выполнение упражнений, аналогичных домашним: № 47 (1; 3), 51.

II. Усвоение понятия простейших логарифмических уравнений и методов их решения

Логарифмическими уравнениями называют уравнения, содержащие переменную под знаком логарифма.

Примеры логарифмических уравнений: lg х = 1 + lg2x, log3(x + 3) = 9, 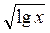= 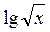и т. д.

Решить логарифмическое уравнение - это значит найти все его корни или доказать, что уравнение корней не имеет.

Простейшее логарифмическое уравнение имеет вид log х = b, где а > 0, а ≠ 1, х > 0. По определению логарифма следует, что х = аb.

Другой вид простейшего логарифмического уравнения таков: loga x = loga b, где а > 0, а ≠ 1, х > 0, b > 0.

Из этого уравнения следует, что х = b. Действительно, из равенства loga x = loga b на основании определения логарифма и основной логарифмической тождества имеем: x = 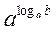= b.

Простейшим логарифмическим уравнением является уравнение logx a = b, где х > 0, х ≠ 1, а > 0.

По определению логарифма имеем: хb = а, отсюда х = .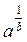

В основном, все логарифмические уравнения, которые мы будем решать, сводятся к решению простейших уравнений.

Пример 1. Решите уравнение log3 (2x + 1) = 2.

Решение

По определению логарифма имеем:

2х + 1 = 32, 2х = 8, х = 4.

Проверка: log3(2 · 4 + 1) = log39 = 2.

Ответ: 4.

Пример 2. Решите уравнение log3x = log3(6 - х2).

Решение

Из равенства логарифмов чисел следует: х = 6 - х2; х2 + х - 6 = 0; х1 = -3, х2 = 2.

Проверка:

1) Число -3 не является корнем данного уравнения, так как выражение log3(-3) - не определен;

2) log3x = log32; log3(6 - х2) = log3(6 - 22) = log32.

Ответ: 2.

Пример 3. Решите уравнение logх+1 (2х2 + 1) = 2.

Решение

По определению логарифма имеем:

2х2 + 1 = (х + 1)2; 2х2 + 1 = х2 + 2х + 1; х2 - 2х = 0; х1 = 0, х2 = 2.

Проверка:

1) Значение х1 = 0 не является корнем данного уравнения, так как основание логарифма х + 1 не должна равняться 1.

2) logх+1(2·22 + l) = log39 = 2.

Ответ: 2.

Отметим, что в описанных примерах используются только такие преобразования, которые не приводят к потере корней, но могут привести к получению посторонних корней. Поэтому проверка каждого из полученных корней обязательна, если нет уверенности в равносильности уравнений.

Коллективное решение упражнений№ 53 (1; 3; 9), 54 (1), 52 (6; 13).

III. Подведение итогов урока

IV. Домашнее задание

Раздел V § 3. Вопросы и задания для повторения раздела V № 26-29. Упражнение № 52 (1-5).