Урок № 56
Тема. Решение задач
Цель: обобщить и систематизировать знания учащихся о определение тригонометрических функций острого угла, их основные свойства, тригонометрические тождества, а также о способах применения полученных знаний во время выполнения упражнений.
Тип урока: применение знаний, умений и навыков.
Наглядность и оборудование: конспект 21.
Ход урока
I. Организационный этап
II. Проверка домашнего задания
Решения задач домашней работы проверяется по образцу и с комментарием.
III. Формулировка цели и задач урока
Тема урока определяет двойную цель урока:
1) закрепление знаний определений тригонометрических функций острого угла, их свойств, а также тождеств для тригонометрических функций определенного острого угла;
2) продолжение работы по формированию умений практического применения этих сведений.
IV. Воспроизведение, коррекция и систематизация опорных знаний
Повторение знаний учащихся, приобретенных ими во время изучения нового материала, частично состоялось в ходе проверки домашнего задания.
Систематизировать знания учащихся можно путем решения таких задач, как задачи на дописывание и на поиск ошибок (примеры таких задач - см. предыдущий урок, этапы формирования знаний и подведение итогов).
V. Формирование умений
Применение знаний в стандартных ситуациях
Самостоятельная работа
Вариант 1
1. По данным рис. 1 найдите cos α.
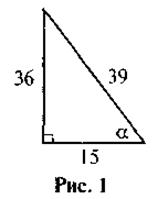
2. По данным рис. 2 найдите х.
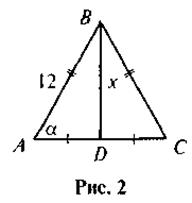
3. По данным рис. 3 найдите х и у.
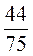
4. По данным рис. 4 найдите АС.
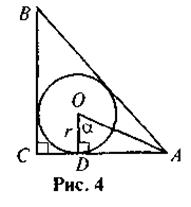
Вариант 2
1. По данным рис. 5 найдите sin a.
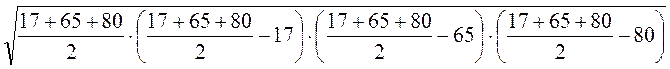
2. По данным рис. 6 найдите х.
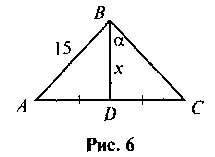
3. По данным рис. 7 найдите х и у.
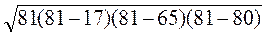
4. По данным рис. 8 найдите АС.
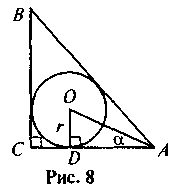
Применение знаний в нестандартных ситуациях
1. Упростите выражение:
а) 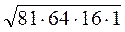 ;
;
б) tg2 α (1 - sin α)(1 + sin α);
в) 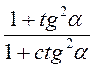 .
.
2. Упростите выражение:
а) (sin α + cos α)2 + (sin α - cos α)2;
б) 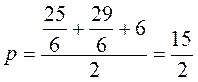 ;
;
в) 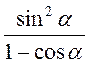 ;
;
г) 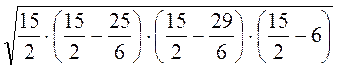 ;
;
д) 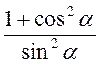 ;
;
e) (1 - sin α)2 + (1 - cos α)2 + (1 + sin α)2 + (1 + cos α)2.
3. Вычислите sin α + cos α, если sin α cos α = 0,48.
4. Упростите выражение:
1) 1 + cos2 α - sin2 α;
2) (1 - cos α)(1 + cos α);
3) 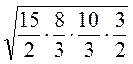 ;
;
4) 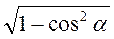 ;
;
5) 2 - cos2 α - sin2 α;
6) 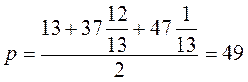 ;
;
7) 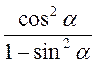 ;
;
8) (sin α - cos α) + 2 sin α cos α;
9) 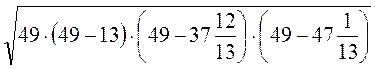 ;
;
10) 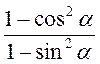 ;
;
11) sin2 α + sin2(90° - α);
12) 1 - cos2(90° - α);
13) sin2 α + tg2 α + cos2 α.
Итогом этого этапа урока является выделение основных типов задач по теме и обобщение способов их решения (независимо от уровня сложности).
VII. Итоги урока
Диагностика усвоения учащимися знаний и умений может быть проведена в форме тестовой работы.
Тестовая работа
1. Из тождеств неправильная?
1) 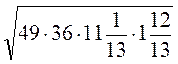 ;
;
2) 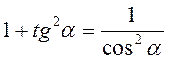 ;
;
3) 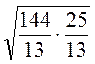 ;
;
4) sin α + cos α = 1.
2. Упростите выражение 1 - cos2 α.
1) (1 - cos α)(1 + cos α);
2) - sin2 α; 3) sin α; 4) sin2 α.
3. Найдите cos α, если sin α = 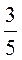 .
.
1) 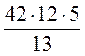 ; 2)
; 2) 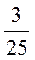 ; 3)
; 3) 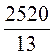 ; 4)
; 4) 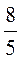 .
.
4. Найдите tg α, если sin α = 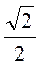 .
.
1) 4; 2) 3; 3) 2; 4) 1.
5. Вычислите значение sin α, если tg α = 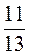 .
.
1) 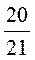 ; 2)
; 2) 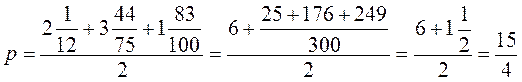 ; 3)
; 3) 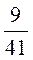 ; 4)
; 4) 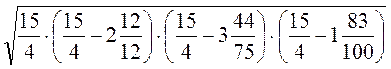 .
.
VIII. Домашнее задание
Повторить содержание основных понятий темы.
Решить задачи.
1. Упростите выражения:
a) (sin α + cos α)2 + (sin α - cos α)2;
б) 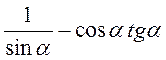 ;
;
в) 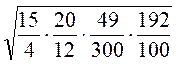 .
.
2. Вычислите:
a) cos 45° sin 45° - sin 30°;
б) sin 60o cos 30° - sin 90°;
в) tg 45° sin 45°;
г) 2 ctg 30° sin 60° - cos 60°.
3. Известно, что sin А + cos
А + cos А = 0,5 . Найдите sin
А = 0,5 . Найдите sin А cos
А cos А.
А.
4. Вычислите:
1) cos α ctg α; 2) sin α · ctg α (0° α 90°), если sin α = 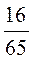 .
.
5. Упростите выражения:
1) (sin α + cos α)2 + (sin α - cos α)2;
2) 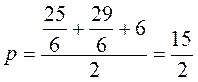 ;
;
3) (1 + sin α + cos α)(sin α + cos α - 1);
4) 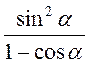 ;
;
5) 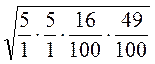 ;
;
6) 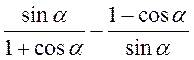 ;
;
7) (1 - sin α)2 + (1 - cos α)2 + (1 + sin α)2 + (1 + cos α)2.