|
III. Формулировка цели и задач урока Толчком к интеллектуальной деятельности учащихся может служить предложенное учителем задание. Задачи. Выполните изображение прямоугольного треугольника с катетами а, b и гипотенузой с. Углы, противоположные катетам а и b, обозначьте соответственно α, β. Запишите отношение, которым равны tgα и ctgα. Сравните записанные отношение. Что вы заметили? Изменится ли результат, если взять другой прямоугольный треугольник? Сформулируйте полученный результат в виде утверждения. Цель предлагаемого задания - наглядно продемонстрировать учащимся существование определенных зависимостей между тригонометрическими функциями некоторого острого угла. Далее учитель подчеркивает, что для других тригонометрических функций (кроме тангенса и котангенса одного и того же угла также существуют определенные зависимости; их изучение и составляет основную цель урока.
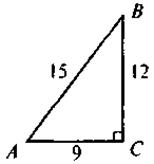
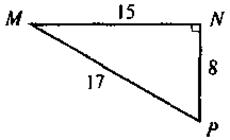
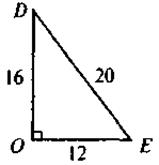
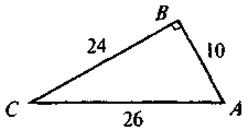
IV. Актуализация опорных знаний С целью формирования сознательного понимания учащимися содержания и схем доказательства тригонометрических тождеств ученики должны повторить содержание теоремы Пифагора, определения синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника. Выполнение устных упражнений 1. Закончите предложения: 1) Если катеты прямоугольного треугольника равны 12 см и 9 см, то гипотенуза равна... 2) Если две большие стороны прямоугольного треугольника равны 17 и 15, то третья сторона равна... 3) Если диагональ квадрата равна 12 см, то сторона квадрата имеет длину... 4) Если диагонали ромба имеют длины 12 см и 16 см, то сторона ромба имеет длину... 2. Выполните задачи за готовыми рисунками
V. Усвоение знаний План изучения нового материала 1. Теорема, выражающая основную тригонометричну тождество. 2. Следствие из основной тригонометрической тождества. 3. Соотношение для тангенса и котангенса одного и того же острого угла прямоугольного треугольника. 4. Примеры задач. @ Содержание нового материала включает в себя формулирование и доведение четырех основных тождеств для тригонометрических функций одного и того же острого угла. Изучение нового материала проводим согласно способу изложения его в учебнике, однако приведенного в учебнике примера на применение изученных тождеств для вычисления значений тригонометрических функций желательно добавить пример на применение изученных формул для преобразования тригонометрических выражений (с демонстрацией приема введения тригонометрической единицы). Проверка понимания учащимися изученных тождеств проводится по вопросам: 1) верно Ли утверждение: сумма квадратов синуса и косинуса острого угла равны 1? 2) верно Ли утверждение: произведение тангенса угла на котангенс угла равен 1? 3) может Ли синус и косинус некоторого острого угла равна соответственно: а) 4) могут Ли тангенс и котангенс некоторого острого угла равна соответственно: а) 5) выражения следует дописать, чтобы равенства стали тождественностями (α, β, γ - некоторые острые углы)?
cos2(α + β) + ... = 1; cos2 β + sin2 β - cos2 α - sin2 α = ...
VI. Формирование первичных умений Выполнение графических упражнений Начертите острый угол. Отметьте на разных сторонах угла две точки и проведите из них перпендикуляры до другой стороны угла. а) Измерьте стороны прямоугольных треугольников, образовавшихся и вычислите двумя способами синус и косинус построенного угла. Сравните результаты. б) Вычислите тангенс построенного угла двумя способами - по значению и соответствующей тригонометричною тождественностью. Сравните результаты. Выполнение письменных упражнений 1. Определите, могут ли синус и косинус одного угла соответственно равнялся-вать: а) 2. Определите, могут ли тангенсі котангенс одного угла соответственно равны: 3. а) 0,4 и 2,5; 4. б) 1,1 и 0,9; 5. в) 6. Найдите: a) sin α, если cos α = б) cos α, если sin α = в) tg α, если sin α = 7. Найдите значения тригонометрических функций острого угла А, если: a) sin А = 8. Упростите выражение: a) 1 - cos2 α; б) tg α cos α; в) 1 + sin α + cos2 α. 9. Упростите выражение: а) б) cos α - cos α sin2 α; в) tg α ctg α - cos2 α. @ Упражнения, которые необходимо выполнить учащимся после изучения нового материала, направленные на закрепление знаний формул, а также на формирование умений использовать изученные формулы при решении задач следующих типов: проверка возможности существования угла с данными значениями тригонометрических функций, вычисление значений тригонометрических функций, применение тождеств для упрощения тригонометрических выражений.
VII. Итоги урока Верны ли приведенные равенства? 1) tg α · cos α = sin α; 2) 1 + cos2 α - sin2 α = 0; 3) 4) sin2 α + cos2 β = 1; 5) tg α · ctg β = 1.
VIII. Домашнее задание Изучить содержание и доказательство теоремы об основной тригонометричну тождество и следствия из нее. Решить задачи. 1. Найдите tg α, если: а) sin α = 2. Упростите выражение: а) 1 - cos2 α; б) 3. Найдите: а) ctg α, если sin α = 0,5; б) tg α, если cos α = 4. Упростите выражение: а)
|
|
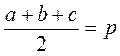
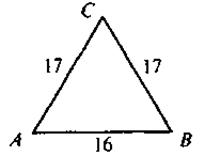
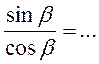 ;
; 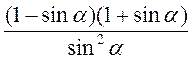 ;
; 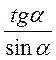 ; в)
; в) 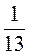 .
.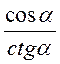 ; б)
; б)