Урок 55
Тема. Угол между плоскостями
Цель урока: формирование понятия угла между плоскостями и умений учащихся находить углы между плоскостями.
Оборудование: стереометрический набор, модель куба.
Ход урока
И. Проверка домашнего задания
1. Фронтальное опрашивание.
1) Что такое угол между прямой и плоскостью?
2) Чему равен угол между прямой и плоскостью, если известно, что прямая:
а) параллельна плоскости;
б) перпендикулярна к плоскости?
3) В каких пределах находится угловая мера угла между прямой и плоскостью?
4) правильно Ли, что:
а) прямая, которая пересекает параллельные плоскости, пересекает их под одинаковыми углами;
б) плоскость, которая пересекает параллельные прямые, пересекающие их под одинаковыми углами?
2. Ответы на вопросы учащихся, возникшие у них при выполнении домашних задач.
Задача № 36.
Дано: АВ = а; АС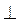 α; 1)
α; 1)  ABC = 45°; 2)
ABC = 45°; 2)  ABC = 60°;
ABC = 60°;  ABC = 30° (рис. 284).
ABC = 30° (рис. 284).
Найти: ВС.
Решение
1) BC = AB cos  ABC = a cos 45° =
ABC = a cos 45° = 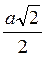 ;
;
2) ВС = AB cos  ABC = a cos60° =
ABC = a cos60° = 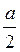 ;
;
3) BC = AB cos  ABC = a cos 30° =
ABC = a cos 30° = 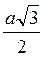 .
.
B и д п о в и д ь. а) 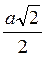 ; б)
; б) 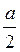 ; в)
; в) 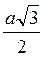 .
.
Задача № 38.
Дано: АО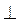 α; АО = a;
α; АО = a;  ABO = 30°;
ABO = 30°;  ACO = 45°;
ACO = 45°;
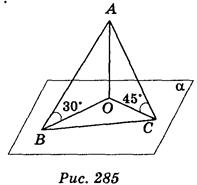
 CAB = 90° (рис. 285).
CAB = 90° (рис. 285).
Найти: ВС.
Решение
1) С ΔАОВ АВ = 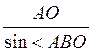 =
= 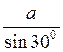 = 2a.
= 2a.
2) Из ΔАОС АС = 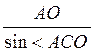 =
= 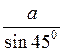 = a
= a .
.
3) Из ΔАВС ВС = 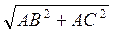 =
= 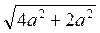 = а
= а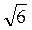 .
.
Ответ. а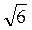 .
.
Задача № 40.
Дано: АО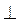 α ; АО = а;
α ; АО = а;  ABO =
ABO =  ACO = 30°;
ACO = 30°;  BOC = 120° (рис. 286).
BOC = 120° (рис. 286).
Найти: ВС.
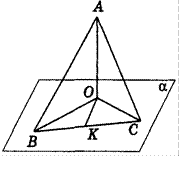
Рис. 286
Решение
1) ΔАОВ = ΔАСО, отсюда BO = CO.
2) Из ΔАОС OC = AO ctg  ACO = a ctg
ACO = a ctg  30° = a
30° = a .
.
3) ΔВОС - равнобедренный. Проведем ОК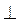 ВС, тогда
ВС, тогда  BOK =
BOK =  KOC = 120° : 2 = 60°.
KOC = 120° : 2 = 60°.
4) С ΔВKС КС = ОС sin  KOC = а
KOC = а sin60° =
sin60° =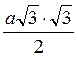 =
=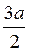 .
.
Тогда ВС = 2КС = 2 · 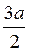 = 3а.
= 3а.
Ответ. 3а.
3. Математический диктант.
SO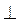 (ABO), SA и SB - наклонные, SO = а , AOB = 90°.
(ABO), SA и SB - наклонные, SO = а , AOB = 90°.
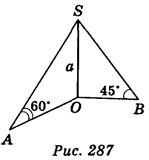
Вариант 1.  SAO = 60°,
SAO = 60°,  SBO = 45° (рис. 287).
SBO = 45° (рис. 287).
Вариант 2.  SAO = 45°,
SAO = 45°,  SBO = 30° (рис. 288).
SBO = 30° (рис. 288).
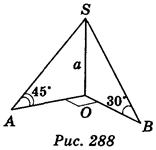
Пользуясь рисунком, найдите:
1) проекцию наклонной SA на плоскость АОВ; (2 балла)
2) длину наклонной SA; (2 балла)
3) проекцию наклонной SB на плоскость АОВ; (2 балла)
4) длину наклонной SB; (2 балла)
5) расстояние между основаниями наклонных; (2 балла)
6) расстояние между прямыми SO и АВ. (2 балла)
Ответ. Вариант 1. 1) 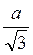 ; 2)
; 2) 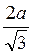 ; 3) а; 4) a
; 3) а; 4) a ; 5)
; 5) 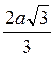 ; 6)
; 6) 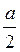 .
.
Вариант 2. 1) а; 2) а ; 3) а
; 3) а ; 4) 2; 5) 2; 6)
; 4) 2; 5) 2; 6) 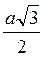 .
.
II. Восприятие и осознание нового материала
Понятие угла между плоскостями
Пусть даны две плоскости α и β, которые пересекаются по прямой с (рис. 289). Проведем плоскость, которая перпендикулярна к прямой с, она пересечет плоскости α и β по прямым а и b. Угол между прямыми а и b называется углом между плоскостями α и β.
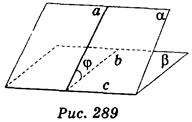
Угол между двумя плоскостями, которые пересекаются,- это угол между прямыми пересечения этих плоскостей с плоскостью, перпендикулярной к линии пересечения данных плоскостей. Если плоскости параллельны, то угол между ними равен 0°. Если плоскости перпендикулярны, то угол между ними равен 90°. Итак, если φ - угол между плоскостями, то 0°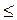 φ
φ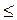 90°. Далее учащиеся самостоятельно знакомятся с доказыванием того, что назван так угол между плоскостями не зависит от выбора секущей плоскости, по учебнику (§ 4, п. 33).
90°. Далее учащиеся самостоятельно знакомятся с доказыванием того, что назван так угол между плоскостями не зависит от выбора секущей плоскости, по учебнику (§ 4, п. 33).
Решение задач
1. Дано изображение куба. Найдите угол между плоскостями АВС и ABD (рис. 290).
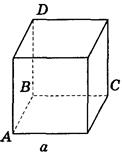
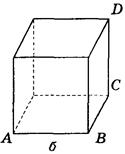
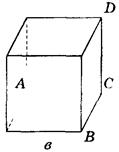
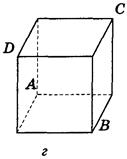
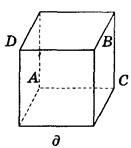
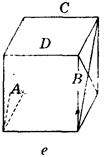
Рис. 290
Ответ, а) 90°; б) 45°; в) arctg 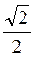 ; г) 2arctg
; г) 2arctg 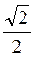 ; д) 0°; е) 90°.
; д) 0°; е) 90°.
2. Задача № 43 из учебника (с. 57).
3. Задача № 44 из учебника (с. 57).
4. Задача № 46 из учебника (с. 58).
5. Задача № 47 из учебника (с. 58).
III. Домашнее задание
§4, п. 33; контрольный вопрос № 16; задачи № 42, 45 (с. 57).
IV. Подведение итога урока
Вопрос к классу
1) Дайте определение угла между плоскостями.
2) зависит Ли величина угла между плоскостями от выбора секущей плоскости?
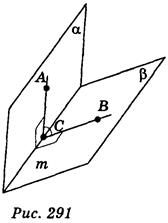
3) Плоскости α и β пересекаются по прямой m (рис. 291), точка А принадлежит плоскости α, точка В - в плоскости β, точка С - прямой m; АС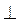 m, ВС
m, ВС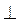 m, ACB = 60°. Укажите, какие из приведенных утверждений правильные, а какие - неправильные:
m, ACB = 60°. Укажите, какие из приведенных утверждений правильные, а какие - неправильные:
а) плоскость АВС перпендикулярна к прямой m;
б) углом между плоскостями α и β является угол между прямыми ВС и m;
в) угол между плоскостями α и β равен углу между прямой АС и плоскостью β;
г) угол между плоскостями α и β больше 60° ;
д) угол между плоскостями α и β равен 120°.