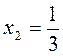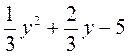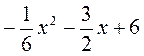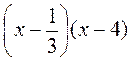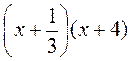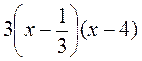|
@ Изучая материал урока по представленному плану, учащиеся должны усвоить определение квадратного трехчлена и уметь отличать его среди других выражений, а также приводить свои примеры квадратных тричленів (этому способствует выполнение соответствующих устных упражнений). Кроме того, учащиеся должны осознать, что задача о отыскания корней квадратного трехчлена сводится к решению соответствующего квадратного уравнения (поэтому перед изучением темы следует организовать повторение материала, связанного с решением квадратного уравнения - см. этап актуализации...). Следует подчеркнуть, что разложение квадратного трехчлена на линейные множители по формуле является еще одним из способов разложения многочленов на множители, который широко применяется в курсе алгебры. Учащиеся должны знать определение квадратного трехчлена, определение корня квадратного трехчлена, формулу разложения квадратного трехчлена на линейные множители. Осознанному восприятию учащимися нового материала может способствовать интерактивная форма записи конспекта урока: в виде диалога - вопрос - ответ.
VI. Формирование умений Выполнение устных упражнений 1. Является ли число 1; 0; 2. Докажите, что квадратный трехчлен х2 + 2 не имеет корней. 3. Имеет ли квадратный трехчлен корни и если имеет, то сколько: а) х2 + 2х + 1; б) х2 + 5; в) х2 - 1; г) -3х + х2? 4. Известно, что а - первый коэффициент, a х1 и х2 - корни некоторого квадратного трехчлена. Представьте трехчлен в виде произведения, если: а) а = 1; х1 = 2; х2 = -3; б) а =3; Выполнение письменных упражнений Для реализации дидактической цели урока следует решить задачи следующего содержания: 1. Нахождение корней квадратного трехчлена. а) x2 + x - 12; б) х2 - 2х - 35; в) 3х2 + 16х + 5; г) 7х2 - 96х - 28; д) х2 - 10х + 18;) 16х2 + 24х + 3; ж) 4х2 - 28х + 49; с) х2 + 3х + 5. 2. Нахождения количества корней квадратного трехчлена. 3. Разложение на множители квадратный трехчлен. Можно разложить на линейные множители квадратный трехчлен? 1) Разложите на множители квадратный трехчлен: а) а2 - 13а + 22; б) -b2 + 2b + 24; в) 100с2 - 50c + 6; г) 2) При каких значениях а можно разложить на линейные множители квадратный трехчлен: а) 2х2 + 7х - а; б) ах2 + 4х + 8; в) 3х2 - 5ах - 1; г) (a - 1)х2 + 6ах + 6? 4. Логические упражнения и задачи повышенного уровня сложности для учащихся, имеющих достаточный и высокий уровни знаний. 1) Разложите на множители трехчлен: а) х2 - 2ху + 63у2; б) 2а2 + 7аb + 3b2; в) 3m2 +11mn - 4n2. 2) Найдите пропущенный выражение:
5. На повторение: выделить квадрат двучлена из выражения. @ Решение задач на нахождение корней, исследование существования корней квадратного трехчлена сводится к решению соответствующего квадратного уравнения (соответствующие сведения активизирована на этапе актуализации). Перед решением задач, требующих разложения квадратного трехчлена на линейные множители, уместно сначала выяснить, возможно ли оно, т.е. определить знак дискриминанта квадратного трехчлена, и только после этого выполнять разложение на множители, если это возможно. Задачи на повторение имеет целью подготовить учащихся к восприятию некоторых свойств квадратного трехчлена, о которых речь пойдет в следующем уроке.
VII. Итоги урока Укажите правильный ответ. 1) Корень трехчлена 3х2 - 13х +4: а) 4; 2) Расписание трехчлена 3х2 - 13х + 4 на линейные множители имеет вид: а)
VIII. Домашнее задание 1. Изучить содержание основных новых понятий, уметь отвечать на вопросы (см. конспект). 2. Решить упражнения на нахождение корней квадратного трехчлена и на разложение квадратного трехчлена на линейные множители. 3. На повторение: теорема Виета и обратная теорема, их применение для решения квадратных уравнений; решить задачи на выделение полного квадрата.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
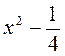 ; в) х2 - х?
; в) х2 - х?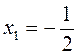 ;
;