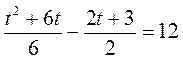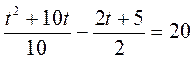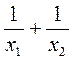Урок № 55
Тема. Тематическая контрольная работа по теме «Квадратные уравнения. Формула корней квадратного уравнения. Теорема Виета»
Цель: проверить уровень усвоения учащимися содержания основных понятий темы «Квадратные уравнения» и уровень умений, сформированных в ходе изучения темы.
Тип урока: контроль знаний и умений.
Ход урока
I. Организационный этап
II. Проверка домашнего задания
Собрать тетради с выполненной домашней контрольной работой (работу проверить и учесть при выставлении тематического бала).
III. Формулировка цели и задач урока
Учитель еще раз может подчеркнуть, что целью контрольной работы является демонстрация учащимися своих учебных достижений, а именно: показать знание содержания основных понятий и алгоритмов, изученных в теме, а также умение применять приобретенные знания при решении упражнений.
IV. Условие тематической контрольной работы
Тематическая контрольная работа Квадратные уравнения. Теорема Виета
Вариант 1 |
Вариант 2 |
1°. Решите квадратное уравнение: |
а) х2 - 5х + 4 = 0; б) у2 + 9у = 0; в) 2t2 - 72 = 0; г) 7z2 - z - 8 = 0 |
a) m2 - 7m + 6 = 0; б) х2 - 6х = 0; в) 6у2 + у - 7 = 0; г) 5t2 - 125 = 0 |
2°. При каких значениях t выполняется равенство: |
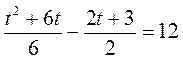 ? ?
|
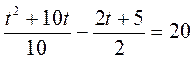 ? ?
|
3*. Один из корней данного уравнения равен 4. Найдите второй корень и число (коэффициент) b: |
y2 - y - b = 0 |
y2 + bу - 8 = 0 |
4*. Составьте квадратное уравнение с целыми коэффициентами, если корни этого уравнения равны: |
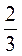 и -1 и -1
|
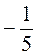 и 2 и 2
|
5*. Не решая уравнение |
|
3x2 - 7x - 11 = 0, |
2х2 + 3х - 13 = 0, |
найдите значение выражения |
|
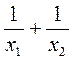
|
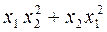
|
V. Итоги урока
Как вариант проведения этого этапа урока можно предложить (после выполнения работы) объявления правильных ответов к заданиям, выполненных учениками, или раздать ученикам для работы дома (домашний анализ контрольной работы) копии правильных решений заданий контрольной работы (заготовленных учителем заранее).
VI. Домашнее задание
1. Выполнить анализ контрольной работы (за розданными разрешениями).
2. Повторить: определение многочлена и сопутствующих понятий, содержание понятия разложения многочлена на множители (по справочнику 7 класса), а также основное свойство дроби и алгоритм сокращение рациональных дробей (за конспектом 8 класса).