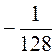УРОК № 55
Тема. Геометрическая прогрессия. Формула n-го члена геометрической прогрессии
Цель урока: закрепить знания учащихся о содержании определения и сопутствующих понятий геометрической прогрессии, а также о ее основных свойства. Дополнить эти знания знанием формулы n-го члена геометрической прогрессии. Закрепить умения: выделять геометрическую прогрессию среди других числовых последовательностей, находить знаменатель геометрической прогрессии, первые несколько членов геометрической прогрессии, а также использовать свойства геометрической прогрессии. Сформировать умение записывать формулу n-го члена геометрической прогрессии, а также решать различные по содержанию задачи на применение этой формулы.
Тип урока: дополнение и закрепление знаний, отработка умений и навыков.
Наглядность и оборудование: опорный конспект № 34.
Ход урока
I. Организационный этап
Учитель проверяет готовность учащихся к уроку, настраивает их на работу.
II. Проверка домашнего задания
Для осознанной работы учащихся на этом этапе урока можно провести проверку домашнего задания по образцу.
Другой вариант проведения этого этапа урока - выполнение тестовых заданий (см. ниже) с последующей проверкой и обсуждением результатов их выполнения, во время которых повторяется содержание основных понятий предыдущего урока, а также схемы применения изученных на этом уроке понятий для решения типовых задач.
Тестовые задания
1. Какая из приведенных последовательностей является геометрической прогрессией?
а) 2; 6; 18; 54;
б) 80; 40; 20; 5;
в) 4; 8; 32; 64;
г) 2; -10; 50; 250.
2. Найдите знаменатель геометрической прогрессии (bn), если b5 = 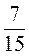 , b6 =
, b6 = 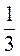 .
.
а) 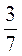 ; б)
; б) 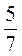 ; в)
; в) 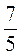 ; г)
; г) 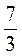 .
.
3. Девятый член геометрической прогрессии равен 12, а знаменатель равен 3. Найдите десятый член геометрической прогрессии.
а) 15; б) 36; в) 39; г) 108.
III. Формулировка цели и задач урока.
Мотивация учебной деятельности учащихся
Так же, как при изучении вопроса о формулу п-го члена арифметической прогрессии, работу на этом этапе урока организуем как коллективный поиск решения задачи: как наиболее рациональным способом найти значение n-го члена геометрической прогрессии, зная ее первый член и знаменатель.
Осознав нерациональность решения задачи известным ученикам способом (через применение рекуррентной формулы), они приходят к вопросу: не существует способа нахождения любого члена геометрической прогрессии без необходимости находить предыдущие несколько ее членов? Поиск ответа на этот вопрос - основная цель урока.
IV. Актуализация опорных знаний и умений учащихся
Устные упражнения
1. Является ли геометрической прогрессией последовательность (хn):
1) 3; 3; 3; 3; 3;
2) 0; 0; 0; 0; 0;
3) 3; 6; 12; 24; 48.
2. Назовите первый, третий и пятый члены последовательности, заданной формулой хn = 64 ∙ 21-n. Является геометрической прогрессией? Чему равна ее знаменатель?
3. Известно, что числа а1; а2; а3; а4; а5 образуют геометрическую прогрессию со знаменателем b. Будет ли геометрической прогрессией последовательность:
1) 2a1; 2а2; 2а3; 2а4; 2а5;
2) а1; а3; а5?
Чему равен знаменатель каждой из этих прогрессий?
V. Дополнение знаний
План изучения нового материала
1. Формула n-го члена геометрической прогрессии.
2. Примеры применение выведенной формулы.
Опорный конспект № 34
Формула n-го члена геометрической прогрессии |
Если (bn) - геометрическая прогрессия, то bn=bl - qn-1,
где b1 - первый член геометрической прогрессии;
q - знаменатель геометрической прогрессии. |
Пример 1. Найдем шестой член геометрической прогрессии (b1): 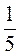 ; 1; 5; ... . ; 1; 5; ... .
Решение
b1 = 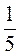 ; q = ; q = 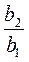 = 5; b6 = b1 ∙ q5 = = 5; b6 = b1 ∙ q5 = 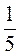 ∙ 55 = 54 = 625. ∙ 55 = 54 = 625.
Ответ: 625. |
Пример 2. Найдем первый член геометрической прогрессии (bn), если b7 = 32; q = -2.
Решение
b7 = b1 ∙ q6 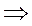 b1 = b1 = 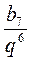 = = 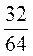 = = 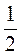 . .
Ответ: 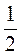 . . |
Пример 3. Найдем знаменатель геометрической прогрессии (bn), в которой b7 = -12, b9 = -108.
Решение
b9 = b1 ∙ q8; b7 = b1∙ q6 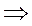 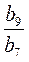 = q2; q2 = = q2; q2 = 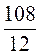 = 9, тогда q = 3 или q = -3. = 9, тогда q = 3 или q = -3.
Ответ: 3 или-3. |
Методический комментарий
Единственный новый момент, который прилагается к изученных на предыдущем уроке определение и свойства геометрической прогрессии - это формула n-го члена геометрической прогрессии, которая выводится через определение, и сама в дальнейшем будет основой для вывода формулы суммы первых п членов геометрической прогрессии (следует отметить, что способ рассуждений, которые проводятся для получения названной в теме урока формулы, является традиционным, так же, как и основные типы задач на ее применение,- см. ниже). Примерное содержание учебного материала помещено в опорном конспект № 34.
VI. Отработка умений
Письменные упражнения
Содержание письменных упражнений урока может быть таким:
1) задачи на прямое применение формулы n-го члена геометрической прогрессии, у которой задан первый член и знаменатель которая задана перечнем первых нескольких своих членов;
2) найти n-й член, если известны несколько первых членов геометрической прогрессии;
3) найти номер некоторого члена геометрической прогрессии или проверить, является ли данное число членом данной геометрической прогрессии;
4) прикладные задачи на применение определения геометрической прогрессии и формулу ее n-го члена.
Методический комментарий
Содержание упражнений и цель их решения такие же, как и на предыдущем уроке: закрепление определения и формулы, изученных на этих уроках, а также выработки оперативных умений применения формул при решении задач в различных ситуациях (если позволяют успехи учащихся, повышается уровень сложности задач за счет задач на применение свойств геометрической прогрессии). Среди задач урока достаточно важное место должны занимать сдачи на составление систем уравнений высших степеней (если позволяет уровень математической подготовки учащихся), а также задачи на применение характеристической свойства геометрической прогрессии.
VII. Итоги урока
Контрольные вопросы
1. Как найти знаменатель геометрической прогрессии, если известны ее первый и второй члены?
2. Как найти третий член геометрической прогрессии, если известны ее первый и второй члены?
3. Как найти шестой член геометрической прогрессии, если известны ее первый член и знаменатель?
VIII. Домашнее задание
1. Изучить содержание материала в опорных конспектах № 33, 34.
2. Выполнить самостоятельную работу (см. ниже) с вариантом, указанным учителем.
Самостоятельная работа
Вариант 1
Решите задачу.
1. Найдите первые четыре члена геометрической прогрессии (bn), если b1 = -2, q = -3.
2. Найдите знаменатель и 5-й член геометрической прогрессии 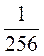 ;
; 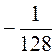 ,
, 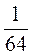 , ... .
, ... .
3. Между числами 16 и 81 вставьте три таких числа, чтобы вместе с данными числами они образовывали геометрическую прогрессию.
4. Найдите первый член и знаменатель геометрической прогрессии (bn), если b10 = 9b8, b3 + b6 = 168, (q > 0).
Вариант 2
Решите задачу.
1. Найдите первые четыре члена геометрической прогрессии (bn), если b1 = 25, q = -0,2.
2. Найдите знаменатель и 5-й член геометрической прогрессии -72; 12; -2; ... .
3. Между числами 64 и 27 вставьте два таких числа, чтобы вместе с данными числами они образовывали геометрическую прогрессию.
4. Найдите первый член и знаменатель геометрической прогрессии (bn), если b10 = 25b8, b2 + b4 = -520 (q > 0).