Часть 2 МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА

Раздел 5 ЯВЛЕНИЯ ПЕРЕНОСА

5.8. Теплопроводность газов

Если газ неравномерно нагрет, то есть когда температура в одной его части выше или ниже, чем во второй, то происходит выравнивание температуры: более нагретая часть охлаждается, в то же время более холодная нагревается.

Это связано, наверное, с потоком теплоты от более нагретой части газа к более холодной. Это явление возникновения потока теплоты в газе (или жидкости) называют теплопроводностью. В любом теле, в частности в газе, на который совершаются внешние воздействия, теплопроводность приводит к выравниванию температур. Этот процесс, как правило, нестационарный. Однако бывают случаи, когда разница температур искусственно поддерживается постоянной.

Чтобы определить количественные закономерности, характеризующие процесс теплопроводности, рассмотрим относительно простую задачу, по своему характеру аналогичную той, которая рассматривалась при изучении диффузии.

Предположим, что температура газа меняется от точки к точке вдоль какого-либо направления в газе, например вдоль оси х, т.е. является функцией координаты х, тогда как в плоскости, перпендикулярной к этой оси, температура везде одинакова (рис. 5.8).

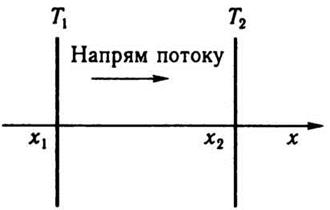
Рис. 5.8

Изменение температуры вдоль оси х характеризуется градиентом 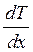. Суть градиента заключается в том, что он равен изменению температуры от одной точки к другой, отнесенной к единице расстояния между ними. Существование градиента температуры является важным условием для возникновения теплопроводности.

Направление потока теплоты совпадает с направлению падения температуры. Если росту координаты х (то есть dх > 0) соответствует уменьшение температуры (dТ 0), то теплота течет в направлении рост х: поток теплоты направлен так, чтобы уменьшить существующий градиент температуры, который его вызвал. Опыт показывает, что поток тепла Q пропорционален градиенту температуры, площади поверхности, которую пересекает, времени протекания (закон Фурье):

Поток теплоты предусматривает ту количество теплоты, протекающей через единичную площадку за единицу времени:

Коэффициент k в выражении (5.23) и (5.24) называют коэффициентом теплопроводности. Как видно из этих уравнений, он численно равен потоку теплоты при градиенте температуры 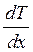, равном единице. Единицы равны также площадь поверхности s и время t, за которое происходит поток теплоты. Из уравнения (5.23) видно, что коэффициент теплопроводности в СИ выражается в джоулях на метр-секунду-кельвин [Дж/(м ∙ с ∙ К)], в системе СГС в ергах на сантиметр-секунду-кельвин [эрг/(см ∙ с ∙ К)]. В технике его часто выражают в кілоджоулях на метр-секунду-кельвин [кДж/(м ∙ с ∙ К)].

Когда на газ, в котором существует градиент температуры, не действуют сторонние силы, то есть к нему извне не подводится энергия, теплопроводность приводит к выравниванию температуры. Сначала рассмотрим нестационарную теплопроводность.