УРОК 55
Тема. Деление с
остачею
Цель: ознакомить
учащихся с правилами деления с остачею, с выражением деления через делитель,
неполную долю и остаток; формировать умения учащихся решать простейшие задачи
наделение с остачею.
Тип урока:
усвоение новых знаний и умений.
Оборудование: таблица
«Деление с остачею».
Ход урока
I. Актуализация
опорных знаний
Устные упражнения
1.
1) Какое
число получим от деления 48 на 6?
2) Делимое 816,
доля 8. Найти делитель.
3) Делитель 3,
доля 24. Найти делимое.
4) Делимое 63,
доля 9. Чему равен делитель?
2. 1) Уменьшающееся на 39 больше вычитаемое.
Чему равна разность?
2) Делитель в 51 раз
меньше делимого. Чему равна доля?
3. Решить уравнения: 1) х · 10 = 0; 2) х ·
0 = 0; 3) (х - 8)(2 - x) = 0.
II. Усвоение знаний
Методические
рекомендации
@ Тема
«Деление с остачею» является непростой, но весьма важной, потому что это база для работы с
дробными числами (преобразование неправильной дроби на дробное число и обратная
действие). Поэтому надо решить много примеров для усвоения основных понятий
(«неполная доля» и «остаток»), а также добиться того, чтобы каждый ученик после
деление «уголком» был в состоянии записать результат в виде a = bq + r.
Постановка проблемы
Чтобы показать ученикам
целесообразность рассмотрения названной действия, им предлагается решить несколько
задач.
Задача 1. Разделить
36 орехов поровну на 7 кучек.
Задача 2. Поделить
20 конфет между шестью друзьями поровну.
Задача 3. Воздушная
шарик стоит 30 к. Сколько таких шариков можно купить на 1 грн.?
Задача 4. За один
день котенок съедает 70 г сухих кормов. На сколько дней хватит ему
400-граммовой коробки корма?
Во время
решение этих задач выясняется, что деление нацело невозможно. Действительно, в
задачи 1, например, 5·7 = 35, а 6·7 = 42, то есть не существует такого натурального
число, от умножения которого на 7 получили бы 36. Деления 36 на 7 невозможно (в
натуральных числах). Разобрав аналогично задаче 2-4, приходим к выводу, что в
многих случаях при решении задач на деление приходится находить не
одно (как это было ранее), а два числа (неполное доля и остаток), которые
удовлетворяют некоторые требования.
Формирование новых
знаний
Если в задаче 1
попробовать разложить 36 орехов на 7 равных кучек, то в каждой кучке будет по 5
орехов и еще 1 орех останется. Если же собрать все 7 полученных кучек, то в них
будет орехов меньше, чем 36 (на 1). Поэтому, чтобы получить 36, надо к произведению 7·5
добавить 1 орех, что остался.
То есть 36 = 7 · 5 +
1 или (далее вывешивается схема «Деление с остачею»).

Учащиеся знакомятся с
понятиями «неполная доля» и «остаток» и выясняют их свойства (см. схему).
@ Обратить
внимание учащихся:
если известны а и b, то q и r находятся выполнением деления а на b;
если известны b, q и r, то а находим по
формуле a = bq+r.
III. Формирование умений
@ № 534. Обязательно требовать от
учеников после записи деления «уголком» делать соответствующую запись в виде а = bq+r, называя найденные числа (неполная доля q и остаток r).
Пример оформления
задач:
|
3)
|
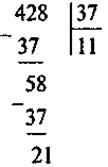
|
428 = 37 · 11 + 21
|
@ № 535. Аналогично записывается деления
«уголком», переходим к записи в форме a = bq+r, затем заполняем
таблицу (или, чтобы сэкономить время, просто подчеркиваем в решении названы в
таблицы числа).
@ № 537. 1) После выполнения этого
раздела обратить внимание на определенную закономерность - остаток числа от деления на 10
совпадает с цифрой в разряде единиц числа; остаток может принимать значения
от 0 (деление нацело) к числу, что меньше b на
1.
@ № 539. После замечаний, сделанных
во время выполнения № 537, ученики легко справятся с этим заданием, но еще раз
надо отметить, что остаток может быть равен 0 (деление нацело).
№№ 541-542. Базовые
задачи на применение действия деления с остачею.
№ 544. Обратившись
к формуле a = bq+r, bq = r - a, имеем: a = 12 · 7 + 9, а = 93.
№ 546.
Записав результат деления уголком или в строку:
82 : 8 = 10 (ост.
2), имеем: 82 = 8 · 10 + 2.
IV. Итог урока
@ Основная
мысль, которую надо донести до учащихся по данной теме: что любые два числа а и b (a ≥ b) можно разделить с
остачею r. В отдельных случаях этот остаток равен 0 (тогда имеем
деление нацело). Во всех других случаях для частицы а : b находим
2 числа q и r (неполная доля и остаток) так, что a = bq + r, причем r b.
Какое число пропущено
в ряду чисел?
|
87
|
10
|
8
|
?
|
|
45
|
6
|
?
|
3
|
|
?
|
5
|
3
|
4
|
V. Домашнее задание
п. 18, № 536; 538;
540; 543; 545.