Урок № 54
Тема. Синус, косинус и тангенс острого угла прямоугольного треугольника
Цель: добиться усвоения учащимися содержания определений синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника и их свойства, вытекающие из теоремы Пифагора, подобия прямоугольных треугольников и свойств сторон прямоугольного треугольника (против большей стороны лежит больший угол, и наоборот). Сформировать умение воспроизводить содержание определений и их свойств, а также находить значения тригонометрических функций острого угла по данным прямоугольного треугольника.
Тип урока: усвоение новых знаний.
Наглядность и оборудование: конспект «Определение тригонометрических функций острого угла».
Ход урока
И. Организационный этап
Как всегда, в начале изучения нового раздела следует предоставить учащимся информацию:
· ориентировочный план изучения раздела;
· количество учебных часов;
· примерное содержание материала;
· основные требования к знаниям и умениям учащихся;
· примерное содержание заданий, которые будут вынесены на контроль.
(Эту информацию можно поместить на стенде «Справочно-информационный уголок» в кабинете математики и с целью экономии времени предложить учащимся для самостоятельного ознакомления в неурочное время).
II. Проверка домашнего задания
Если дома ученики выполняли письменное задание (анализ решения задач контрольной работы или коррекционную работу и т.п.), то правильность выполнения этой работы учитель проверяет, собрав тетради учеников на проверку.
III. Формулировка цели и задач урока
Чтобы сформулировать цель урока, достаточно слов учителя о том, что в науке и технике часто решают задачи, в которых по известным стороной и углом прямоугольного треугольника надо найти неизвестные его стороны и углы, или наоборот, зная стороны прямоугольного треугольника, вычислить его углы. Примером таких задач являются хорошо известные задачи на применение соотношений между катетом, лежащим против угла 30°, и гипотенузой, рисунки в которых представлены ниже (см. рис. 1).
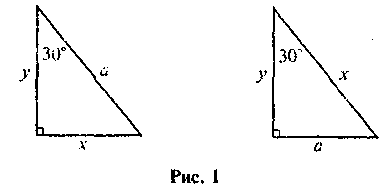
Найдите х, у, если а - известное.
Решение этих задач демонстрирует зависимость между длиной катета, противоположным углом 30° и длиной гипотенузы, то есть зависимость между сторонами прямоугольного треугольника и его углом. Рассуждая последовательно, можно предположить существование общих зависимостей между сторонами и углами прямоугольного треугольника, которые. могут быть записаны в алгебраическом виде и одним из частных случаев которых есть известное соотношение между длиной катета, противоположным углом 30° и длиной гипотенузы. Итак, цель урока определяется как необходимость изучения соотношений между сторонами и углами прямоугольного треугольника и изучение их свойств, а также освоения способов применения этих соотношений при решении задач.
IV. Актуализация опорных знаний
С целью формирования сознательного понимания учащимися содержания определений отношений между сторонами и углами прямоугольного треугольника и их свойства учащиеся должны повторить содержание определение прямоугольного треугольника и его элементов (понятие катета, лежащего против данного острого угла, и катета, прилегающий добавленного угла), признаков подобия прямоугольных треугольников и свойства сторон подобных треугольников.
Повторение этого материала можно провести в форме беседы или во время выполнения устных упражнений.
Выполнение устных упражнений
На рис. 2 найдите все пары подобных прямоугольных треугольников и докажите их подобие. В каждом треугольнике назовите наименьший катет и угол, лежащий против этого катета, а также угол, что является прилегающим к этого катета.
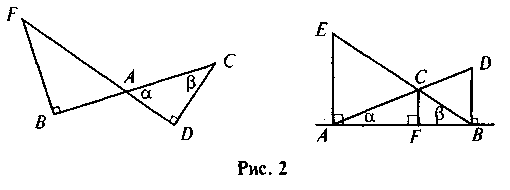
V. Усвоение знаний
План изучения нового материала
1. Определение синуса острого угла прямоугольного треугольника. Его обозначение.
2. Определение косинуса острого угла прямоугольного треугольника. Его обозначение.
3. Определение тангенса острого куга прямоугольного треугольника. Его обозначение.
4. Определение котангенса острого угла прямоугольного треугольника. Его обозначение.
5. Свойства тригонометрических функций острого угла прямоугольного треугольника.
@ Изучения соотношений между сторонами и углами в прямоугольном треугольнике традиционно начинается с введения понятий синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника и формулировка и доведение их свойств (зависимость числовых значений только от меры угла). В этом плане теоретический материал нового учебника не отличается от традиционного содержания соответствующего раздела предыдущего учебника. Однако, в связи с изменением последовательности изучения материала по новой программе по сравнению с предыдущей, обоснование свойств синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника изменилось. Теперь сформулированы свойства очень легко доказываются с ссылкой на подобие прямоугольных треугольников (треугольники с общим острым углом подобные по признаку, следовательно, их соответствующие стороны пропорциональны по определению подобия треугольников).
Следует отметить, что в новом учебнике содержится дополнительный материал относительно семантики понятий «синус», «косинус», «тангенс»; этот материал может помочь учащимся быстрее запомнить содержание определений этих понятий.
Среди свойств, которые используются в задачах и которые необходимо увидеть «между строк», необходимо выделить свойство, которое следует из того, что в треугольнике против большего угла лежит большая сторона, и наоборот. Это свойство - рост синуса острого угла за роста угла и убывания косинуса острого угла за роста угла - на этом этапе изучения тригонометрии может быть сформулирована в виде утверждения: большему острому углу прямоугольного треугольника соответствует большее значение синуса и меньше значения косинуса. Изучение содержания теоретического материала урока уместно проводить согласно учебника по плану, представленному выше. Во время изучения вопроса о способе обозначения тригонометрических функций следует сразу, предупреждая типичные ошибки учеников, объяснить, что эти обозначения являются сокращенной записью соответствующего названия латинскими буквами (например, sin α - это сокращение выражения «синус угла альфа»), а не произведение. Кроме того, поскольку не существует абстрактных понятий синуса, косинуса, тангенса и котангенса (эти понятия обязательно ассоциируются с определенным острым углом прямоугольного треугольника), то и записи типа sin, cos и т.п. просто не имеют смысла.
Добиться понимания учащимися содержания изученного материала и его закрепления можно путем выполнения упражнений (см. ниже), предложенных учащимся во время изучения нового материала.
1. Один из учеников 8 класса начертил на доске прямоугольный треугольник с катетами 30 см и 50 см и вычислил значение синуса, косинуса, тангенса и котангенса острого угла, что лежит против меньшего катета. Затем к доске вышел другой ученик и сказал, что начертит прямоугольный треугольник с катетами 45 см и 75 см, в котором синус, косинус, тангенс и котангенс острого угла, противоположного наименьшего катета, будут большими, потому что его больший треугольник. Не ошибается ли этот восьмикласним? В чем его ошибка?
2. Какие из чисел: 1; 0,5; 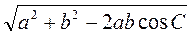 ;
; 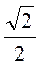 ;
; 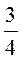 ;
; 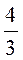 ; 0; -0,3 могут быть числовыми значениями синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника? Объясните.
; 0; -0,3 могут быть числовыми значениями синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника? Объясните.
3. Прочитайте записи: sin A = 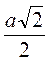 ; соs B =
; соs B = 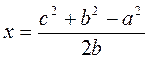 ; tg γ = 1; ctg φ = 2. Объясните, что они означают.
; tg γ = 1; ctg φ = 2. Объясните, что они означают.
После обсуждения вопросов следует провести обобщение способов применения изученного материала, если надо найти значение синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника, то используют определение этих понятий; если же надо ответить на вопрос относительно данных значений тригонометрических функций, то следует использовать их свойства. В изучении нового материала пользуемся конспектом.
Конспект 21 |
Определение тригонометрических функций острого угла.
Тригонометрические тождества
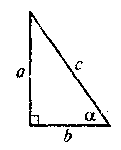
Если 0 α 90° - острый угол прямоугольного треугольника, а - противоположный катет; b - прилежащий катет, с - гипотенуза, то sin α = 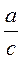 , cos α = , cos α = 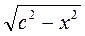 , tg α = , tg α = 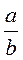 , ctg α = , ctg α = 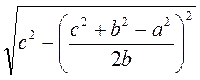 . . |
|
Свойства
1) 0 cos α 1, 0 sin α 1, tg α > 0, ctg α > 0.
2) Если 0 α β 90°, то sin α sin β, cos α > cos β, tg α tg β.
3) Какой α = β, то sin α = sin β, cos α = cos β, tg α = tg β, сtg α = ctg β. |
Тригонометрические тождества |
1) sin2α + cos2α = 1 => 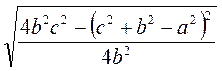 , , 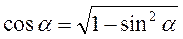 ; ;
2) 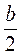 , , 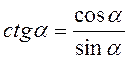 , tg α · ctg α = 1. , tg α · ctg α = 1. |
VI. Формирование первичных умений
Выполнение устных упражнений
1. По рисунку 3 определите, какая тригонометрическая функция угла К выражается отношением:
а) 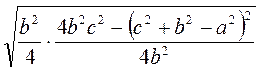 ; б)
; б) 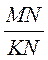 ; в)
; в) 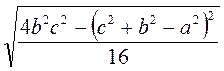 .
.
2. В прямоугольном треугольнике KMN (рис. 3) KN > MN. Который из острых углов треугольника имеет больший синус; больший косинус; больший тангенс?
3. Может ли синус острого угла прямоугольного треугольника равен 0,99; 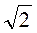 ,
, 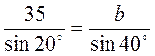 - 2?
- 2?
4. Может ли произведение синуса и косинуса одного угла равняться единице? А произведение тангенса и котангенса?
5. Может ли тангенс острого угла прямоугольного треугольника равен  ; 0,01; 100?
; 0,01; 100?
Выполнение письменных упражнений
1. Начертите с помощью транспортира прямоугольный треугольник с острым углом 40°. Измерьте его стороны и вычислите синус, косинус и тангенс этого угла.
2. Постройте прямоугольный треугольник ABС, в котором:
а) tg А = 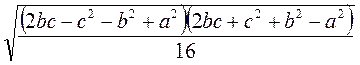 ; б) sin А =
; б) sin А = 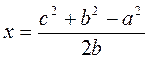 .
.
3. Постройте угол 75°. С помощью дополнительных построений и измерений найдите синус, косинус, тангенс и котангенс этого угла.
4. Постройте острый угол ос, если:
a) sin α = 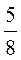 ; б) cos α =
; б) cos α = 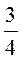 .
.
5. Докажите, что для любого острого угла A tg A > sin A.
6. Катеті гипотенуза прямоугольного треугольника соответственно равны 6 см и 10 см. Найдите:
а) синус острого угла, что лежит против большего катета;
б) косинус острого угла, прилегающего к меньшего катета;
в) тангенс острого угла, что лежит против большего катета.
@ Выполнении всех упражнений имеет целью закрепление учащимися изученной терминологии и изученных свойств, а также понимание сферы применения изученного материала (см. вывод предыдущего этапа урока). Решение задач предусматривает дополнительное повторение теоремы Пифагора для вычисления неизвестной стороны прямоугольного треугольника перед применением изученных определений.
VII. Итоги урока
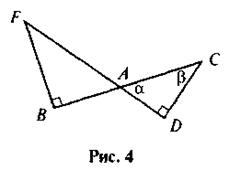
Подайте разными способами косинус, синус и тангенс углов α и β (рис. 4).
VIII. Домашнее задание
Изучить содержание определений синуса, косинуса, тангенса острого угла прямоугольного треугольника и доказательства их свойств.
Решить задачи.
1. Начертите острый угол. Отметьте на одной стороне угла две точки и проведите из них перпендикуляры до другой стороны угла.
а) Измерьте стороны прямоугольных треугольников, образовавшихся и вычислите двумя способами синус построенного угла. Сравните результаты.
б) Вычислите косинус построенного угла двумя способами - по значению и по основной тригонометричною тождественностью. Сравните результаты.
2. Катеты прямоугольного треугольника равны 8 см и 15 см. Вычислите синус, косинус и тангенс наименьшего угла треугольника.
3. Высота равнобедренного треугольника, проведенная к основанию, равна 5 см, а длина основания - 24 см. Найдите синус, косинус, тангенс и котангенс угла при основании треугольника.
4. Докажите, что для любого острого угла A cos A ctg А.
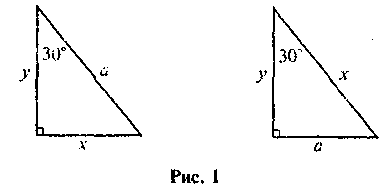
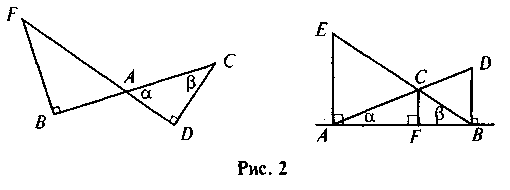

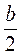 ,
, 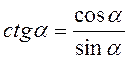 ,
, 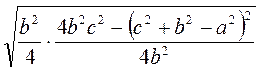 ; б)
; б) 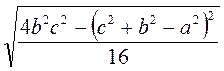 .
.
