Урок № 54
Тема. Применение различных способов разложения многочленов на множители
Цель: отработать навыки применения специальных приемов и классических методов разложения многочленов на множители; продолжать знакомство учащихся со сферой применения разложения многочленов на множители; обобщить и систематизировать полученные по теме знания и умения и навыки.
Тип урока: комбинированный.
Ход урока
I. Организационный момент
Проверяем готовность учащихся к уроку, сообщить план работы.
II. Проверка домашнего задания
@ Предложенное домашнее задание не является простым для учащихся, поэтому следует проверить его тщательно; учащиеся задают вопросы и вместе с учителем ищут ответы на них.
Особое внимание обращаем на задание № 1 (3, 4, 5) и 2 (4), потому что в № 1 (3) имеем разницу кубов (не совсем знакомо, по крайней мере на предыдущем уроке таких задач не было).
№ 1 (4) - имеем сразу два полные квадраты (новое!).
№ 1 (5) - традиционно сложное, потому что надо «увидеть» выражение, противоположный полном квадрату.
№ 2 (4) - обязательно разобрать, потому что содержит такой контрольный момент: деление на выражение с переменной сужает ОДЗ уравнения, а следовательно, может привести к потере корня уравнения.
III. Формулировка цели и задач урока
@ Соответствии с определенным на первом уроке плану, на этом отрабатываем навыки применения различных способов и приемов разложения многочленов на множители и расширяем сферу применения приобретенных умений и навыков, а также обобщаем и систематизируем свой опыт.
IV. Актуализация опорных знаний
Фронтальная беседа
1. Что значит разложить многочлен на множители?
2. Какие способы разложения многочленов на множители вы знаете?
3. Какие из названных способов разложения многочленов на множители и в каком порядке использовать, чтобы представить в виде произведения такие выражения:
1) х2 - ху;
2) х2 - у2;
3) х3 - х;
4) х2 - 2х + 1;
5) х3 - 2х2 + х;
6) х2 - 2х + 1 - у2;
7) х2 - у2 + 2х - 2у;
8) х3 - х2 + х - 1;
9) (х - 1)2 - х2?
V. Работа с опережающим домашним заданием
Задача 1. Выделите полный квадрат в выражении:
1) х2 + 2х - 8;
2) а2 - 8а + 12;
3) 4с2 - 4с - 3;
4) х2 - 6ху + 5у2;
5) а2 + 12аb + 11b2;
6*) (х - 1)2 - 6(х - 1) + 8.
Задание 2. Подайте выражение, стоящее после полного квадрата, в виде квадрата некоторого выражения. Прочитайте выражение, что образовался. Что общего имеют данные выражения? Как их разложить на множители?
Сделайте выводы.
@ Если вся подготовительная работа проведена должным образом, то вывод, который делают учащиеся, может быть примерно таким, к которому хочет подвести учеников учитель, а именно: чтобы разложить трехчлен на множители по формуле разности квадратов двух выражений, можно использовать прием «выделение полного квадрата двучлена».
Задача 3. Разложите данные тричлени на множители:
1) х2 + 6х + 8;
2) х2 + 12х + 35;
3) х2 - 10х - 24;
4*) х2 - 7х + 12.
(4*) - контрпример - в этом тричлені удобнее разбить-7х на два слагаемых и сгруппировать, потому-7х имеет нечетный коэффициент.)
VI. Усвоение умений и навыков
@ Решаем упражнения достаточного и высокого уровней сложности. Если уровень подготовки учащихся достаточно высокий и соответствующий темп выполнения, то можно предложить несколько специфических приемов работы с выражениями: перегруппировка и т.д.
Выполнение письменных упражнений
1. Разложите на множители:
1) х2 - 4х + 3;
2) х2 + 2х - 8;
3) t2 + t - 6;
4) k4 + 6k2 + 5;
5) u4 + 2u2 - 35;
6) (3x2 - 4)2 - 8(3x2 - 4) - 9.
2. Разложите на множители:
1) (х - у)(х + у) + 2(2х - у) + 3;
2) (х - у)(х + у) + 2(3х - 2у) + 5.
3. Решите уравнение:
1) х2 - 8х + 7 = 0;
2) у2 + 12у + 20 = 0;
3) (х - 1)2 + 6(х - 1) + 8 = 0;
4) (х - 1)(х - 3)(х2 - 3) = (x - 1)(х - 3).
4. Докажите, что значение выражения 334 + 992 - 330 - 990 делится на 80.
5*. Известно, что а + b = 5, ab = 4. Найдите значение выражения:
1) a2b + ab2; 2) a2 + b2; 3) a3 + b3.
VII. Итоги урока
@ Важнейшим итогом является формирование у учащихся правильного понимания: 1) строения системы форм и методов (способов) разложение многочленов на множители; 2) сферы применения названных понятий и способов действий на уроках математики (или там, где речь идет о математические объекты: числовые и буквенные выражения, уравнения и т.п.).
Поэтому желательно этот этап урока посвятить именно систематизации и обобщению знаний и умений учащихся.
Учитель может подготовить заранее (или делать записи во время беседы) карточки с записями основных понятий по теме «Разложение на множители»: вынесение общего множителя за скобки и т. д.
Учитель предлагает учащимся назвать основные математические понятия, которые усваиваются в ходе изучения этой темы (для оживления работы можно устроить «Математический аукцион» - см. математика, 6 кл.), и соответственно открывает карты (или делает запись на доске).
После того как будут названы все понятия, предлагаем ученикам расположить эти карточки в порядке, что соответствует логике темы (последовательность применения способов и т.п.), и классифицируем виды задач, которые были решены в этой теме. В конце концов можно все соображения представить в виде схемы:
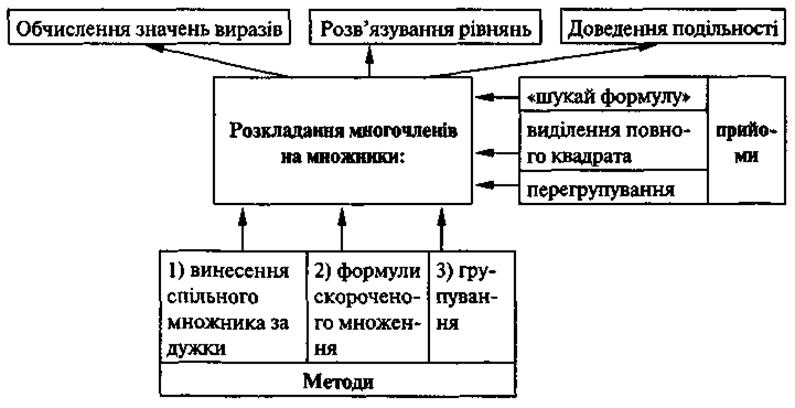
VIII. Домашнее задание. Домашняя самостоятельная работа
№ 1. Разложите на множители:
1) 6а3 - 6а;
2) 2х2 + 24ху + 72у2;
3) а3 - ab - a2b + a2;
4) х2 + 2ху + у2 - 49;
5) а3 + 8 - а2 - 2а;
6) m3 + 27n5 + m2 + 6mn + 9n2;
7) а2 - b2 + 4а + 4;
8) х2 - 2х - 3;
9) х2 + 4х - 5.
№ 2. Решите уравнение:
1) х2 - 2х - 35 = 0;
2) х3 - 9 = х - 9х2.
№ 3. Докажите, что значение выражения 1110 + 4 ∙749 + 1111 - 4 ∙748 делится на 12.
Дополнительно: поработать со схемой - см. «Итоги» (усовершенствование).