Урок № 53
Тема. Применение различных способов разложения многочленов на множители
Цель: отработать навыки применения различных способов разложения многочленов на множители; ознакомить учащихся со сферой применения разложения многочленов на множители как методического приема.
Тип урока: усвоение умений и навыков.
Ход урока
I. Организационный момент
@ Учитель побуждает учащихся к самопроверке готовности к работе; фиксирует фамилии отсутствующих и сообщает учащимся план работы на уроке.
II. Проверка домашнего задания
@ Для того чтобы проверка домашнего задания была эффективной, желательно не только проверить ответы (эту работу можно доверить ученикам-консультантам, которые сделают проверку к уроку), но осознать действия, что привели к этим ответам. Поэтому на этом этапе можно предложить учащимся следующую самостоятельную работу: с № 1 домашнего задания отдельно выписать номера тех задач, в которых:
1) вынесен за скобки общий множитель, а затем применен формулу разности квадратов;
2) вынесен за скобки общий множитель, а затем применен формулу квадрата разности (суммы) и т. д.
По выполнении этой работы учащиеся проводят самопроверку (правильные решения могут быть розданы или спроецированы на доску при наличии ТСО), а затем, в случае необходимости - коррекцию.
III. Формулировка цели и задач урока
@ На предыдущем уроке в начале изучения темы были выделены три основные задачи, цели. На этом уроке мы обращаемся к 2) и 3) пунктов (см. предыдущий урок).
IV. Актуализация опорных знаний, умений, навыков
Выполнение устных упражнений
1. Прочитайте выражения:
(0,1 х + у)2; (0,1 х)2 + у2; (0,1 х)2 - у2; (0,1 х)3 + у3; (2х)3 - у3.
2. Разложите на множители:
1) a2 - 5ab;
2) а2 - 25;
3) а2 - 0,36;
4) а2 + 4аb;
5) а3 - 125; 6) 64 - х3;
7) 
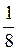- а3;
8) а3 - 25а;
9) х2 - 6х + 5;
10) х22 -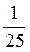 
х20;
11) m3 + 2m2 + m;
12) х2n - 2n+2;
13) (а + 1)2 - 1;
14) (а + 1)2 - b2.
@ Желательно во время выполнения задания 2 устных упражнений комментировать свои действия в соответствии с алгоритмом применения различных способов разложения многочленов на множители.
V. Работа с опережающим домашним заданием
Учащиеся получают задания на заранее приготовленных индивидуальных карточках, это задание выполняется самостоятельно, а потом, как обычно, презентуется, корректируется, и на основании проделанной работы, формулируются выводы.
Задачи. Каждый из выражений:
1) х2 - 2ху + у2 - z2;
2) с2 + 9 - 6с - k2;
3) m2 + 2mn + n2 - k2;
4) а2 - 8а - b2 +16;
5) а2 - b2 + а + b (записать в столбик);
6) 4х2 + у - 2х - у2;
7) с2 - b2 + с - b
подайте в виде алгебраической суммы двух многочленов (многочлена и одночлена) так, чтобы одно из слагаемых представлял собой полный квадрат двучлена, или разность квадратов. Результаты занесите в таблицу |
Данное выражение |
Его представление в виде суммы полного квадрата одночлена и |
Коррекция |
Его представление в виде суммы разницы квадратов и некоторого одночлена |
Коррекция |
Пример
1) х2 - 4ху + 4у2 - m2 |
(х2 - 4ху + 4у2) - m2 |
|
(х2 - m2) + (-4ху + 4у2) |
|
VI. Изучение нового материала: знакомство с новыми способами действий
@Учитель предлагает задания.
Разложите на множители:
1) х2 - 2ху + у2 - z2;
2) а2 - b2 + а - b;
3) bх4 - х4 + bх3 - х3.
После проведения предварительного этапа урока большинство учащихся поймет, что делать, для других можно показать способ рассуждения, основанный на работе с алгоритмом разложения многочлена на множители с применением различных способов, то есть ход рассуждений может быть таким:
1) х2 - 2ху + у2 - z2 |
= (x2 - 2xy + y2) - z2
1) общего множителя нет;
формулы нет;
группируем, чтобы в группах был или общий множитель (невозможно) или формула (возможны такие группы: 1, 2, 3 и 4) или 1 и 4 и 2 и 3 (нет выхода); |
(х - у)2 - z2 = (x - y - z)(x - y + z)
2) имеем формулу разность квадратов |
2) a2 - b2 + a - b |
= (а2 - b2) + (а - b)
1) см. выше, но группы такие: 1 и 2, 3 и 4, потому что в 1-й группе - формулы |
= (а - b)(а + b) + (а - b) = (a - b)(a + b + 1)
2) имеем общий множитель (а - b), выносим его за скобки |
Выводы. Примеры показывают, что алгоритм (см. предыдущий урок), к сожалению, срабатывает не всегда, поэтому надо знать о возможности использования приема, представленный этими двумя (см. выше) примерами. Этот прием можно назвать «ищи полный квадрат или разность квадратов».
3) bх4 - х4 + bx3 - х3 |
= (bx4 - x4) + (bх3 - х3)
= x4(b - 1) + x3(b - 1) =
1) имеем стандартное разложение методом группировки: группируем 1 и 2, 3 и 4 |
= (b - 1)(х4 + х3)
= x3(b - 1)(x + 1)
2) второй множитель имеет общий множитель х3 |
VII. Усвоение умений и навыков
@ He забываем отрабатывать прием «ищи квадраты».
Выполнение письменных упражнений
1. Разложите на множители:
1а. 1) с2 + 9 - 6с - k2; 2)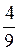 
х2 - а2 - 2аb - b2; 3) 4х2 - 4у - у2 - 4;
1б. 1) х2 - а2 + х - а; 2) 4х2 + у - 2х - у2; 3) 3,5х2 - 3,5у2 - х + у;
1в. 1) х2 - у2 + (х + у)2; 2) а2 + (а + 4)2 - 16; 3) 8а3 - 27b3 + 4a2 - 12ab + 9b2.
2. Решите уравнение:
1) х3 - х = 0;
2) 1,6у3 - 0,4 в = 0;
3) х3 - 4х2 - 4х + 16 = 0;
4) 2z3 - z2 = 8z - 4;
5) х4 - х3 - х2 + х = 0;
6) х3 - 2х2 + 4х - 8 = 0.
3* (дополнительно). Логическая упражнение на повторение.
Найдите пропущенное число или выражение:
15 - 4b
5b + 1 |
3b + 1 = 13
8 - 3b = 2 |
-1
? |
VIII. Итоги урока
Впишите пропущенные выражения, чтобы цепочка равенств стал правильным:
(m - 2)2 + m2 - 4 = (m - 2)2 + (...)(...) = (m - 2)((...) + (m + 2)) = (m - 2)(...) = 2m(...).
IX. Домашнее задание
№ 1. Разложите на множители:
1) а2 - 2аb + b2 - 25;
2) х2 - 16b2 + 8bс - с2;
3) а3 - 27 + а2 - 3а;
4) 4х2 - 12ху + 9у2 - 4а2 - 4ab - b2;
5) b10 - 25b8 - 40b4 -16;
6) х2 - у2 - 6х + 9.
№ 2. Решите уравнение:
1) х3 - 4х = 0;
2) 1,2z3 - 0,3z = 0;
3) х3 - х2 - 9х + 9 = 0;
4*) 4у3 - у2 = 4у - 1 (ни в коем случае не делить на (4у - 1) - потеряем корень)
№ 3. Опережающее домашнее задание.
1. Повторите (за конспектом или учебником), что означает термин «выделить полный квадрат»).
2. Выделите полный квадрат в выражении:
1) х2 + 2х - 8;
2) а2 - 8а + 12;
3) 4с2 - 4с - 3;
4) х2 - 6xв + 5y2;
5) a2 + 12ab + 11b2;
6*) (х - 1)2 - 6(х - 1) + 8.
Замечания. В примере 6* можно для удобства заменить (х - 1) другим выражением, например, выделить полный квадрат относительно в, а затем выполнить обратную замену.