Урок 54
Тема. Угол между прямой и плоскостью
Цель урока: формирование понятия угла между прямой и плоскостью, а также умений учащихся находить углы между прямой и плоскостью.
Оборудование: стереометрический набор, модель куба.
Ход урока
И. Проверка домашнего задания
1. Фронтальное опрашивание.
1) Дайте определение угла между скрещивающимися прямыми.
2) зависит Ли угол между скрещивающимися прямыми от выбора прямых, которые пересекаются и параллельны данным мимобіжним прямым?
3) Сформулировать обобщенное определение перпендикулярности прямой и плоскости.
4) Сформулируйте обобщенную признак перпендикулярности прямой и плоскости.
5) Сформулируйте обобщенную теорему о трех перпендикуляры.
2. Проверка решения задачи № 32.
Решение
Спроектируем ортогональное прямые а, b, с на плоскость, которая параллельна им, получим прямые а1, b1, с1 соответственно, которые попарно пересекаются и параллельные прямым а, b, с. Возможны два случая (рис. 279).
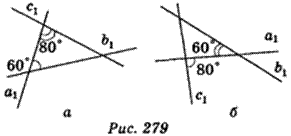
В случае «а» имеем: угол между прямыми b1 и с1 равна 180° - 60° - 80° = 40°.
В случае «б» имеем: угол между прямыми b1 и с1 равна 180° - (180° - 80°) - 60° = 20°.
А за то что b || b1, с || c1, угол между прямыми b и с может равняться или 40° или 20°.
Ответ. 20° или 40°.
3. Решение задач.
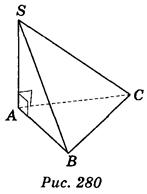
1) Грани SAB и SAC тетраэдра SABC (рис. 280) - прямоугольные треугольники с прямым углом с вершиной в точке А. Докажите, что ребра ВС и AS взаимно перпендикулярны.
2) Дан куб ABCDA1B1C1D1. Докажите, что плоскость, которая проходит через точки А, В1, D1, перпендикулярна к диагонали А1С.
II. Восприятие и осознание нового материала
Угол между прямой и плоскостью
В курсе геометрии 10 класса мы рассмотрели случаи размещения прямой и плоскости: 1) прямая лежит в плоскости; 2) прямая параллельна плоскости; 3) прямая перпендикулярна к плоскости. Остается исследовать случай, когда прямая пересекает плоскость, но не перпендикулярна к ней.
Такие прямые могут быть наклонены к плоскости под разными углами. Что же понимают под углом между прямой и плоскостью?
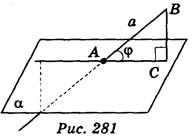
Если прямая параллельна плоскости или принадлежит ей, то считают, что угол между прямой и плоскостью равен 0°. Если прямая перпендикулярна к плоскости, то угол между ними равен 90°. В остальных случаях углом между прямой и плоскостью называют угол между прямой и ее проекцией (ортогональной) на плоскость. На рис. 281 ВС α, А - точка пересечения прямой а с плоскостью α, тогда угол между прямой а и плоскостью α равен углу ВАС = φ. Если φ - угол между прямой и плоскостью, то 0°
α, А - точка пересечения прямой а с плоскостью α, тогда угол между прямой а и плоскостью α равен углу ВАС = φ. Если φ - угол между прямой и плоскостью, то 0° 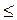 φ
φ 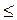 90°.
90°.
Решение задач
1. Задача № 35 из учебника (с. 56).
2. Дано изображение куба. Найдите угол между плоскостью АВС и прямой а (рис. 282).
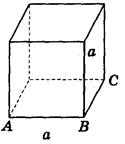
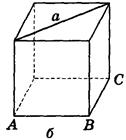
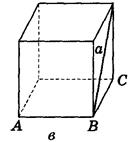
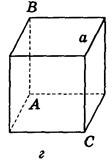
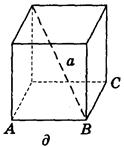
Рис. 282
(Ответ а) 90° ; б) 0°; в) 45° ; г) 45° ; д) arctg 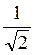 ).
).
3. Задача № 37 из учебника (с. 57).
4. Задача № 39 из учебника (с. 57).
5. Задача № 41 из учебника (с. 57).
6. Задача № 34 из учебника (с. 56).
III. Домашнее задание
§4, п. 32; контрольный вопрос № 15; задачи № 36, 38, 40 (с. 57).
IV. Подведение итога урока
Вопрос к классу
1) Дайте определение угла между прямой и плоскостью.
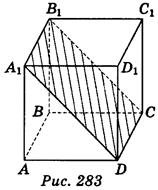
2) В кубе ABCDA1B1C1D1 проведено сечение секущей плоскостью, проходящей через точки А1, D, С (рис. 283). Укажите, какие из приведенных утверждений правильные, а какие - неправильные:
а) плоскость A1DB1 перпендикулярна к прямой АА1;
б) угол между прямой AD и плоскостью A1DC, равен 45°;
в) угол между прямой АВ и секущей плоскостью равен 0°;
г) угол между прямой BC1 и плоскостью A1DC равен 90°.