ГЕОМЕТРИЯ
Раздел ІІ. СТЕРЕОМЕТРИЯ
§24. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ В ПРОСТРАНСТВЕ.
1. Прямоугольная система координат в пространстве. Координаты точки.
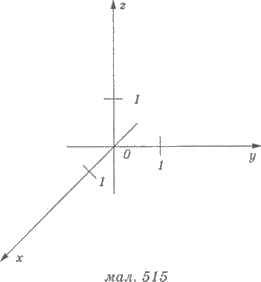
Проведем через точку О пространства три
попарно перпендикулярные прямые х, у, z
(рис. 515). На каждой из прямых выберем
направление, которое обозначим стрелкой
и единицу измерения.
Таким образом задают прямоугольную систему координат в пространстве. Точку О называют
началом координат, а прямые с выбранными направлениями осями координат (или
координатными осями). Ось х называют осью абсцисс, ось у - осью ординат,
ось z - осью аппликат. Начало координат
разбивает каждую из осей на две полуоси - положительную (которую обозначают стрелкой) и
отрицательную. Плоскости, проходящие соответственно через оси координат х и
в, в и
z, х и
z называют координатными плоскостями
ху, у, z, хz.
В прямоугольной системе координат в
пространстве каждой точке М пространства ставится в соответствие единственная упорядоченная
тройка чисел, а каждой упорядоченной тройке чисел - единственная точка пространства. Эту
тройку чисел называют координатами точки. Определяются они аналогично
координатам точки на плоскости.
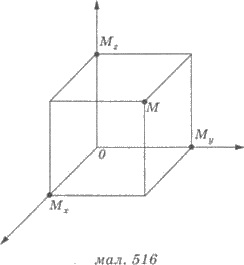
Проведем через точку М плоскость,
перпендикулярную к оси х (рис.
516). Она пересекает
ось х в точке Мx. Координатой х точки М (абсциссой
точки М) называют число, равное по абсолютной величине длине отрезка
ОМx; положительное, если точка Мх
лежит на положительный полуоси х и отрицательное, если она лежит на отрицательной полуоси. Если
же точка М совпадает с точкой О, то считаем, что абсцисса точки М равна А.
Проведем плоскости, перпендикулярные
осям у и z, которые пересекают эти оси в точках Мy иz соответственно. Аналогично
координаты х точки М определяются координата у точки М (ординаты точки М) и
координата z точки М (апліката точки М).