ГЕОМЕТРИЯ
Раздел ІІ. СТЕРЕОМЕТРИЯ
§23. КОМБИНАЦИИ ГЕОМЕТРИЧЕСКИХ ТЕЛ.
6. Многогранник, описанный вокруг шара.
Многогранник называют описанным
вокруг шара, если все его грани касаются поверхности шара.
При этом шар называют вписанной в
многогранник.
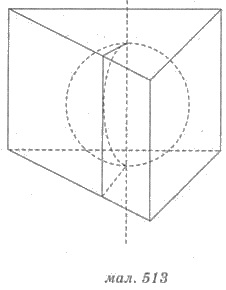
Основные свойства призмы, описанной
вокруг шара, такие (рис. 513):
1) Шар можно вписать в прямую
призму, если ее основанием является многоугольник, в который можно вписать круг, а высота
призмы равна диаметру этой окружности.
2) Центр шара является серединой высоты
призмы, соединяющей центры окружностей, вписанных в многоугольники оснований призмы.
Пример 1. Известно, что в треугольную
призму, стороны оснований которой равны 13 см, 14 см и 15 см, можно вписать шар.
Найти радиус этого шара.
Решения. 1) Диаметр вписанной
шара равен высоте призмы и в то же время равна диаметру круга, вписанного
в основание призмы. Следовательно, радиус окружности, вписанной в основание призмы равна радиусу
шаре.
2) Радиус окружности r, вписанной в основание призмы,
найдем по формуле r = S/p,
где S - площадь треугольника основания, г - его
полупериметр.
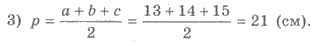
4) По формуле Герона
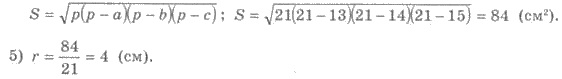
6) Следовательно, радиус шара равен
4 см.
Сформулируем основные свойства
пирамиды, описанной вокруг шара (рис. 514).
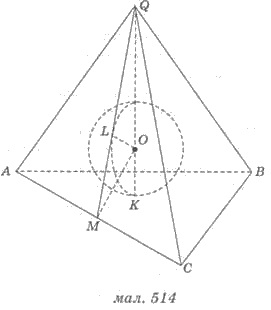
1) Если в пирамиде все двугранные
углы при основании равны между собой, то в эту пирамиду можно вписать сферу. Центр
сферы принадлежит высоте пирамиды, точка соприкосновения с основанием пирамиды совпадает с
центром вписанной в основание окружности, а точки соприкосновения с боковыми гранями принадлежат
высотам этих граней.
2) В любую правильную пирамиду
можно вписать шар. Центр шара принадлежит высоте пирамиды.
3) Центр шара, вписанного в правильную
пирамиду, совпадает с центром окружности, вписанной в равнобедренный треугольник,
боковой стороной которого является апофема правильной пирамиды, а высотой - высота
пирамиды. Радиус шара равен радиусу этого круга.
Пример 2. Известно, что в треугольную
пирамиду, высота которой равна 20 см, а высота одной из боковых граней 25 см,
можно вписать шар. Найти ее радиус.
Решения. 1) Пусть QK - высота треугольной пирамиды QABC, а QM - высота боковой грани (рис. 514). По условию QK = 20 см, QM = 25 см.
2) По условию в пирамиду можно вписать
пулю. Пусть центр этого шара - точка
О, а точка L
- точка касания шара к
боковой грани QAC,
L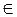 
QM.
3) Обозначим OK = OL
= r - радиус вписанного шара.
4) Прямоугольные треугольники ВУМ и OLM уровне (за катетом и гипотенузой).
Поэтому 
OMK = OML, а следовательно, МО - биссектриса угла QMK, а потому и треугольника QMK.
5) По свойству биссектрисы
треугольника имеем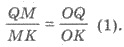 
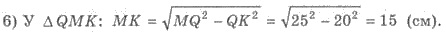
7) Учтем, что OQ = QКАК - ОК, и подставим в равенство (1):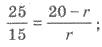 
отсюда
r = 8 ∙ 4/7 (см).
Заметим, что в геометрии
рассматривают также другие комбинации геометрических тел (например, цилиндра и
пирамиды, шара и цилиндра и т.д.).