|
Дарья предложила несправедливый вариант.
Задача 2. Количество возможных вариантов - 36.
II. Актуализация опорных знаний Устные упражнения 1. Какие из названных событий являются достоверными? невозможными? случайными? а) Вода (замерзает) превращается в лед при 0°С; б) после лета наступает зима; в этом году на Харьковщине получат хороший урожай пшеницы. Приведите свои примеры невозможных, достоверных, случайных событий. 2. Перед вами три шкатулки с пуговицами: в первой - 20 пуговиц, во второй - 30, третий - 40 пуговиц, среди которых один - красный. С которой ящика легче всего вынуть, не глядя, красный пуговица? а) первой; б) второй; в) третьей; г) одинаково сложно с любой. 3. Вам предложили купить электронные часы за 1 грн с дополнительным условием: вы платите 1 грн, а потом подбрасываете трижды игральный кубик. Если все три раза выпадет 6 баллов, то часы ваш, в противном случае часы остается продавцу. По вашему мнению, какими словами можно охарактеризовать событие «Часы достанется вам»? а) Практически достоверно; б) практически невозможно; в) рівноможливо с событием «Часы остается вам»; г) утруднюся с ответом. 4. Запишите в процентах числа: 0,52; 0,05; 2;
III. Усвоение знаний 1. Мотивация учебной деятельности @ Проводим беседу, в которой несмотря на того, что мы сделали при решении устных упражнений, еще раз повторяем основные понятия, которые были рассмотрены на предыдущих уроках темы. Но в конце подводим итог, что до сих пор мы только говорили о виды событий и сравнивали шансы наступления нескольких событий. Возникает вопрос: А можно «измерить» шанс наступления события и если можно, то как? 2. Формирование знаний @ Шестиклассники еще не готовы для восприятия строгого определения классической вероятности (которое дается в 11 классе), но на интуитивном уровне понятие о вероятности как числовую характеристику частоты наступления того или иного события они воспринимают. Поэтому план беседы, которую проводим дальше может быть таким: 1) Вероятность как числовая характеристика частоты появления событий или число, которое является отношением количества последствий, ведущих к наступлению данного события, к числу всех возможных последствий. 2) Вероятность достоверного и невозможной событий. 3) Примеры задач на вычисление вероятностей событий.
Беседа 1) Под вероятностью случайного события мы понимаем число, которое характеризует частоту появления данного события. Например Если при условии 100 подбрасываний монеты герб выпал 52 раза, то вероятность выпадения герба равна Если же мы не в состоянии провести много одинаковых экспериментов, чтобы таким образом найти вероятность события, вероятность можно вычислять по следующей схеме: а) Найдем количество всех возможных вариантов, которые имеют одинаковые б) Найдем количество вариантов, которые ведут к появлению данного события. в) Найдем вероятность р по формуле: р = 2) Например Задача 1. Какова вероятность того, что наугад вырванный из нового календаря лист соответствует 30-му числу, если в году 365 дней? Решения. Поскольку в году 365 дней, в календаре 365 листов, вырываем один наугад, то равные шансы вырвать любой из этих 365 листов; поэтому n = 365. В году 12 месяцев, но только в 11 есть 30-е число (исключение - февраль), поэтому листов, что удовлетворяют условие всего 11, следовательно, m = 11. Имеем: р =
IV. Усвоение умений Устные упражнения 1. В ящике лежит 10 шаров, три из которых белые. Какова вероятность того, что наугад один шарик - белая? 2. Из букв разрезной азбуки составлено слово «три». Затем буквы перемешивают и наугад берут одну за другой. Найдите вероятность, что будет составлено исходное слово. 3. Из ящика, в котором 4 белых, 3 черных и 7 красных шаров, выньте один шарик. Какова вероятность того, что она: а) белый; б) черный; в) красная?
Письменные упражнения Задача 1. Все буквы украинского алфавита написаны на 32 одинаковых карточках. Какова вероятность того, что написано на карточке буква будет на обозначение гласного, если карточка извлекается наугад? Задача 2. Какова вероятность того, что наудачу выбранное натуральное число от одного до 30 включительно является делителем числа 30? Задача 3. Из 25 экзаменационных билетов, которые пронумерованы числами от 1 до 25, наугад выбирают один. Какова вероятность того, что номер вытянутого билета есть число, кратное трем? Задача 4. Двое должны поделить между собой 5 одинаковых орехов. Один из них прячет орехи в две коробки любым возможным способом, а другой выбирает любую коробку. Какова вероятность того, что тот, кто отгадывает, получит 3 орехи. Что более вероятно: получит он орехи или нет?
V. Итоги урока В ящике лежат 10 шаров: 3 черные, а другие белые. Какова вероятность того, что из ящика наудачу вынут: а) одну белую; б) одну черную; в)* два белых шарика.
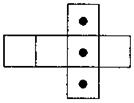
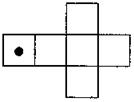
VI. Домашнее задание Повторить: определение достоверных, невозможных и случайных событий; сравнения шансов событий графическим способом и с помощью вариантов. Задача 1. На тарелке лежат 8 одинаковых на вид пирожков: три - с мясом, остальные - с повидлом. Какой пирожок более вероятно взять, если брать пирожки наугад: с повидлом или с мясом? Задача 2. На 5 отдельных карточках написаны буквы слова «шторм». Карточки перемешивают и наугад берут одну за другой. Какова вероятность того, что мы составим данное слово? Задача 3. Одновременно бросают две игральные кости, развертки которых изображены на рис.
Если сверху появится грань с нарисованным кружочком, то это означает, что выпал один балл; если же на верхней грани ничего не изображено - ноль баллов. Сравните шансы появления суммы 0, 1, 2 балла (сумма баллов берется на обеих костях). Изобразите шансы графически.
|
|