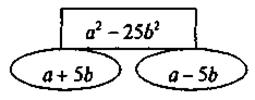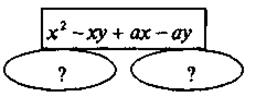Урок № 52

Тема. Применение различных способов разложения многочленов на множители

Цель: систематизировать и обобщить знания и умения учащихся относительно различных способов разложения многочленов на множители; выработать умение применять различные способы разложения многочленов на множители.

Тип урока: систематизация и обобщение знаний.

Ход урока

I. Организационный момент

@ Учитель:

1) проверяет готовность учащихся к уроку;

2) сообщает оценки за тематическую контрольную работу № 5;

3) отвечает на вопросы по заданиям тематической контрольной работы, возникшие у учащихся.

II. Проверка домашнего задания

Работа с опережающим домашним заданием.

Вопрос к классу

1) Что называется разложением многочлена на множители?

2) Какое свойство умножения используют во время вынесения общего множителя за скобки?

3) В какой последовательности выполняется разложение многочленов на множители способом группировки?

4) Какие алгоритмы используют во время разложения на множители многочленов вида а2 - b2; a2 ± 2ab + b2; а3 ± b3?

После беседы проводится самостоятельная работа по заполнению таблицы

По окончании этой работы - проверка (презентация) с последующей коррекцией.

Чтобы сделать необходимые выводы, побуждаем учащихся к сравнение полученных комментариев, после чего - обобщаем выводы.

III. Формулировка цели и задач урока

@ Основную цель трех уроков, объединенных темой «Применение различных способов разложения многочленов на множители», можно сформулировать так: 1) обобщить и систематизировать знания и умения по применению каждого из изученных трех способов разложения многочленов на множители, освоить способы действий по комплексному применению этих способов во время разложения многочленов на множители; сформулировать (если это возможно) определенный алгоритм действий в ходе решения такого вида задач; 2) ознакомиться со спектром задач, решение которых предполагает применение различных способов разложения многочленов на множители; 3) выработка устойчивых навыков применения различных способов разложения многочленов на множители и решение соответствующих задач.

Задание на урок можно определить как первую часть общего учебного задания по теме (см. выше).

IV. Усвоение новых знаний

Понятно, что овладение знаний относительно различных способов разложения многочленов на множители и умений их применять на практике является очень важным для успешного изучения многих наук. Том, чтобы помочь ученику сориентироваться в безграничном пространстве различных выражений, которые раскладываются на множители, мы будем пытаться дать определенный алгоритм, отметив, что он является примерным, то есть как и любое правило, он имеет несколько исключений.

@ Если знания о различные способы разложения многочленов на множители и умение применять эти знания на практике у учащихся на данный момент произведены, единственное, что остается учителю - это вместе с учениками попытаться сформулировать единый алгоритм выполнения действий (последовательность применения изученных способов) во время разложения многочленов на множители. После удачно выполненной работы с опережающим домашним заданием эта процедура не должна вызывать у учащихся трудностей, и формулировка алгоритма является логическим завершением проделанной работы.

Количество примеров, рассмотренных учителем, может быть другой, но автор умышленно взял именно такие примеры, чтобы убедить учащихся в справедливости алгоритма. Желательно, чтобы ученики сравнили ход решенных упражнений и сами убедились в этом.

Также важно обратить внимание на такой момент, чтобы предупредить ошибки, которых традиционно допускают учащиеся при решении задач по теме: разложение многочлена на множители считается законченным, если он представлен в виде произведения или линейных множителей (степень 1) или множители более высокого степеня далее одним из известных семиклассникам способов не разлагаются. Этот момент также выделяем во время объяснения.

V. Усвоение умений

Выполнение письменных упражнений

@ Нa уроке традиционно отрабатываем применение сформулированного алгоритма и решаем соответственно упражнения на его применение.

1. Разложите на множители:

1а. 1) 7а2 - 7b2; 2) km2 - kn2; 3) 9х2 - 36; 4) 4а3 - 4а; 5) х4 - х2; 6) са2 - 9сb2; 7) 2а3 - 2b3; 8) 27с + b3с.

1б. 1) 3р2 + 6гq + 3q2; 2) - b2 + 2bс - с2; 3) 81 - 54b + 9b2; 4) 2xb2 + 8хb + 8х; 5) 9а3 + 6а2 + а; 6) m - 10m2 + 25m5.

1в. 1) 3mn + 24n - 9m - 72; 2) -4abc - 32bc - 12ac - 96c; 3) 1,5а2 - 0,5а2х + 1,5 ах - 0,5ах2; 4) х2у2а - х2у2 + 5аху - 5ху.

2. Решите уравнения: 1) 8х2 - 72 = 0; 2) 12х2 - 3 = 0.

3. Разложите на множители, найдите значение выражения:

1) 4х2 - 4у2, если х = 51, в = 49; 2) 5а2 - 10аb + 5b2, если а = 7,3, b = 2,3.

4* (дополнительно). Логическое упражнение.

Вставьте пропущенные слова, числа, выражения или рисунки:

VI. Итоги урока

Блиц-тест

1. В каком случае указано правильное разложение многочлена 25х2 - 25у2 на множители:

1) 25(х2 - у2);

2) (5х - 5у)(5х + 5у);

3) 25(х - у)(х + у);

4) 25(х - у)2 ?

2. Восстановите логическую цепочку (расставьте выражения 1) - 4) в порядке, что соответствует логике урока):

1) 2у3(у - а + аb - bв);

2) 2у3(1 - b)(в - а);

3) 2y3(y(1 - b) - a(1 - b));

4) 2y4 - 2y3a + 2y3ab - 2y4b.

Какой шаг вы бы добавили к образованному цепочки?

VII. Домашнее задание

Используя теорию и практические навыки, полученные на уроке, выполните задание.

№ 1. Разложите на множители:

1) 14 - 14m2;

2) 3a - 3a3;

3) 7х5 - 7xy2;

4) 5x2y2 - 45а2b2;

5) 3х2 - 24ху + 48у2;

6) -3n4 - 12n3 - 12n2;

7) 2а3 + 54b6;

8) 3х3 - 3ху - 3х2 + 3х2у;

9) 0,2х4 + 0,6х3у - 0,4х3 - 1,2х2у.

№ 2. Найдите значение выражения:

1) 3m2 + 6mn + 3n2, если m = 4,8, n = 5,2;

2) 10а2 - 10b2, если а = 69, b = 31.

№ 3 (опережающий). В данных выражениях (цепочках) выделите группы одночлен, чтобы они образовали выражение, что есть или полным квадратом двучлена или разностью квадратов двух выражений:

1) х2 - 2ху + у2 - z2;

2) с2 + 9 - 6с - k2;

3) m2 + 2mn + n2 - k2;

4) a2 - 8a - b2 + 16;

5) а2 - b2 + а + b;

6) 4х2 + у - 2х - у2;

7) с2 - b2 + с - b.