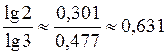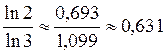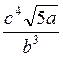УРОК 54

Тема. Основные свойства логарифмов

Цель урока. Изучение основных свойств логарифмов. Познакомить учащихся с логарифмуванням и потенцированием выражений.

И. Проверка домашнего задания

1. Три ученика воспроизводят решение упражнений № 4, 6, 18.

2. Устное решение упражнений на вычисление логарифмов с использованием таблицы 22 для устных вычислений.

Таблица 22

3. Ответы на вопросы, возникшие у учащихся во время выполнения домашнего задания.

II. Восприятие и осознание основных свойств логарифмов

При выполнении преобразований выражений, содержащих логарифмы, при вычислениях и при решении уравнений, неравенств часто используются свойства логарифмов.

Для любых а > 0, а ≠ 1 и любых положительных х и у выполняются равенства:

1. logа l = 0;

2. logаa = 1;

3. logа xy = logа x + logа y;

4. logа = logа x - logа y;

5. logа х р = p logа x (г R);

6. = loga x (p R);

7. loga x = (b > 0, b ≠ 1).

Докажем равенства 3-7. По основной логарифмической тождеством

(И)

(II)

Перемножив равенства (I) и (II), получаем: ху = · = ,

отсюда по определению логарифма имеем loga xy = loga x + loga y.

Следовательно, логарифм произведения равен сумме логарифмов.

Разделив равенства (I) и (II), получаем: = ,

отсюда по определению логарифма имеем: loga = loga x - loga в.

Следовательно, логарифм доли равен разности логарифмов.

Поднеся левую и правую части равенства (И) в степень с показателем р, имеем: (III)

отсюда по определению логарифма имеем: logа х р = p logа x.

Следовательно, логарифм степени равен произведению показателя степени на логарифм основания этой степени.

Из равенства (III) имеем: , отсюда по определению логарифма имеем:

, тогда p; .

Формула 7 называется формулой перехода от одного основания логарифма к второй основы. Докажем ее.

По правилу логарифмирования степени (формула 5) и основной логарифмической тождественностью получаем: ,

отсюда logb х = loga х · logb a или loga = .

С помощью формулы 7 можно находить логарифмы, с произвольным основанием а, имея таблицы логарифмов, составленных для какой-нибудь основанию b. Наиболее употребляемыми являются таблицы десятичных и натуральных логарифмов.

III. Осмысление основных свойств логарифмов

1. Рассмотрим примеры использования формул 3-7. Вычислим:

1) log6 18 + log6 2 = log6(18 - 2) = log6 36 = 2;

2) log12 48 - log12 4 = log6 = log12 12 = 1;

3) log6 = log6 = log6 3 = · 1 = ;

4) log125 5 = log125 5 = log5 5 = · 1 = ;

5) = log4 16 = log4 42 = 2 log4 4 = 2 · 1 = 2.

2. Используя калькулятор (или таблицы), вычислим:

1) log3 2 = ;

2) log3 2 = .

3. Выполнение упражнений № 29, 30.

IV. Восприятие и осознание логарифмирование и потенцирование выражений

Действие нахождения логарифма числа (выражения) называется логарифмуванням.

Пример. Прологарифмуйте выражение у = .

Решение

lg y = lg = lg (a2b2) - lg c3 = lg a2 + lg b2 - lg c3 = 2 lga + 2 lg b - 3 lg c.

Действие, обратная логарифмирования, называется потенцированием.

Потенцирование - нахождение числа (выражения) по его логарифмом.

Пример. Пропотенціюйте выражение lg х = lg 5а - 3 lg b + 4 lg c.

Решение

lg x = lg 5a - 3 lg b + 4 lg c;

lg x = lg - lg b3 + lg c4;

lg x = lg - lg b3 + lg c4; lg x = lg ( · с4) - lg b3;

lg x = lg ; x = .

Выполнение упражнений№ 24 (4), 31 (4).

V. Подведение итогов урока

VI. Домашнее задание

Глава V § 1. Вопросы и задания для повторения № 6-14. Упражнения№ 24 (2), 27, 28, 31 (3).
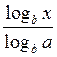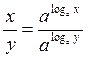
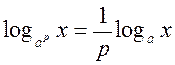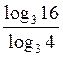