ГЕОМЕТРИЯ

Раздел ІІ. СТЕРЕОМЕТРИЯ

§23. КОМБИНАЦИИ ГЕОМЕТРИЧЕСКИХ ТЕЛ.

4. Пирамида, описанная вокруг конуса.

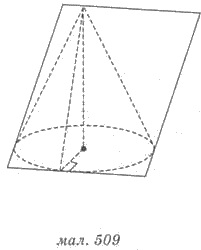
Касательной плоскостью к конусу называют плоскость, проходящая через образующую конуса и перпендикулярная к плоскости осевого сечения, содержащей эту образующую (рис. 509).

Пирамиду называют описанной вокруг конуса, если ее основа описана вокруг основания конуса, а вершиной является вершина конуса (рис. 510).

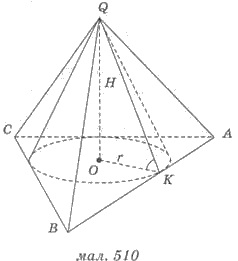
При этом конус называют вписанным в пирамиду. Заметим, что боковые грани пирамиды принадлежат плоскостям, касательным к конусу.

Исходя из определения, имеем свойства пирамиды, описанной вокруг конуса.

1) Конус можно вписать в пирамиду, если ее основанием является многоугольник, в который можно вписать круг, а высота пирамиды проходит через центр этого круга.

2) Радиус основания конуса равен радиуса окружности r, вписанной в основание пирамиды, а высота конуса Н равна высоте пирамиды.

Пример. В основе пирамиды лежит прямоугольный треугольник с катетами 6 см и 8 см, а двугранные углы при основании пирамиды равны 60º. Найти высоту конуса, вписанного в пирамиду.

Решения. 1) Пусть в треугольную пирамиду с основанием АВС и вершиной Q вписан конус (рис. 510). Основа высоты конуса точка О - центр окружности, вписанной в ∆АВС.

2) Пусть точка К - точка касания окружности, вписанной в ∆АВС к стороне АВ. Обозначим ОК = R - радиус окружности, вписанной в ∆АВС, и также радиус основания конуса.

3) ОК АВ, по теореме о трех перпендикуляры QК АВ, поэтому QКО - линейный угол двугранного угла при ребре основания пирамиды. По условию QКО = 60°.

4) По известной формуле радиус круга, вписанного в прямоугольный треугольник, находится по формуле 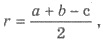где а, b - катеты, с - гипотенуза.

5) По условию АС = 6 см, ВС = 8 см - катеты.

Тогда гипотенуза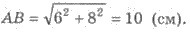

6) Имеем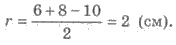

7) QO - высота пирамиды и конуса. В 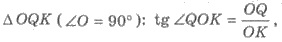тогда