ГЕОМЕТРИЯ
Раздел ІІ. СТЕРЕОМЕТРИЯ
§23. КОМБИНАЦИИ ГЕОМЕТРИЧЕСКИХ ТЕЛ.
3. Пирамида, вписанная в конус.
Пирамиду называют вписанную в конус,
если ее основание вписано в основание конуса, а вершиной является вершина конуса (рис. 508).
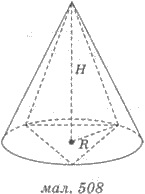
При этом конус называют описанным
вокруг пирамиды.
Понятно, что боковые ребра пирамиды,
вписанной в конус, являются созидательными конуса.
Свойства пирамиды, вписанной в
конус, такие:
1) Конус можно описать вокруг
пирамиды, если ее основанием является многоугольник, вокруг которого можно описать окружность, а высота
пирамиды проходит через центр этого круга.
2) Радиус основания конуса равен
радиуса окружности R, описанной вокруг основания пирамиды, а
высота конуса Н равна высоте пирамиды.
Пример. Вокруг пирамиды, стороны
основания которой равны 10 см, 10 см и 12 см, а высота 8 см, описан конус.
Найти площадь осевого сечения конуса.
Решения. 1) Пусть радиус основания
равен R, а высота - Н (рис. 508).
Тогда площадь осевого
сечения конуса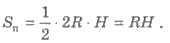 
2) Высота конуса равна равна
высоте пирамиды, поэтому Н = 8 см.
3) Радиус конуса найдем как радиус
круга, описанного вокруг треугольника со
сторонами 10 см, 10 см
и 12 см. Используем формулу R = abc/4S, где
а, b, с
- стороны треугольника, S - его площадь.
4) По формуле Герона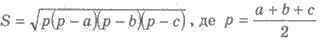 
- полупериметр треугольника.
Имеем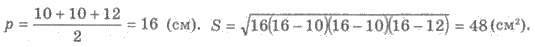 
5) Тогда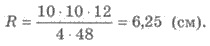 
6) Тогда 