ГЕОМЕТРИЯ

Раздел ІІ. СТЕРЕОМЕТРИЯ

§23. КОМБИНАЦИИ ГЕОМЕТРИЧЕСКИХ ТЕЛ.

2. Призма, описанная вокруг цилиндра.

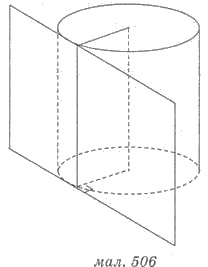
Касательной плоскостью к цилиндру называют плоскость, проходящая через образующую цилиндра и перпендикулярная к плоскости осевого сечения, содержащей образующую цилиндра (рис. 506).

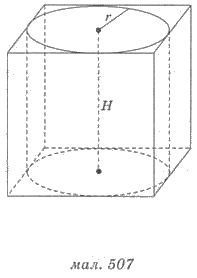
Призму называют описанной вокруг цилиндра, если ее основания описаны вокруг оснований цилиндра, а боковые грани принадлежат плоскостям, касательным к цилиндру (рис. 507).

При этом цилиндр называют вписанным в призму, так как образующие цилиндра перпендикулярны к плоскости оснований, то боковые грани призмы, содержащие образующие, также перпендикулярны к плоскостям оснований, то есть призма, описанная вокруг цилиндра, является прямой.

Из определения призмы, описанной вокруг цилиндра, имеем ее свойства:

1) Цилиндр можно вписать в прямую призму, если ее основанием является многоугольник, в который можно вписать круг. При этом радиус цилиндра r равен радиусу этого круга.

2) Высота Н призмы, которая соединяет центры окружностей, вписанных в основания, принадлежит оси цилиндра.

Пример. Вокруг цилиндра, высота которого равна 5 см, описано четырехугольную призму, три стороны основания которой в порядка следования равны 3 см, 4 см и 7 см. Найти площадь боковой поверхности призмы.

Решения. 1) Обозначим неизвестную сторону четырехугольника основы х. Поскольку этот четырехугольник описан вокруг окружности (рис. 507), то 3 + 7 = 4 + х, отсюда х = 6 см.

2) Площадь боковой поверхности призмы S_бич = Р ∙ l, где Р - периметр основания, l - боковое ребро, равное высоте цилиндра. Имеем: Р = 3 + 7 + 4 + 6 = 20 (см).

3) S_бич = 20 ∙ 5 = 100 (см²).