ГЕОМЕТРИЯ

Раздел ІІ. СТЕРЕОМЕТРИЯ

§23. КОМБИНАЦИИ ГЕОМЕТРИЧЕСКИХ ТЕЛ.

Нами уже рассмотрены простые геометрические тела: призма, пирамида, цилиндр, конус, шар. Но в природе, технике и геометрии также рассматривают и комбинации указанных геометрических тел.

1. Призма, вписанная в цилиндр.

Призму называют вписанной в цилиндр, если ее основания вписаны в основания цилиндра, а боковые ребра являются созидательными цилиндра (рис. 505).

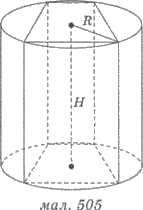
При этом цилиндр называют описанным вокруг призмы. Понятно, что поскольку образующие цилиндра перпендикулярны к плоскости основания, то призма, вписанная в цилиндр, является прямой.

Из определения призмы, вписанной в цилиндр, вытекают его свойства:

1) Цилиндр можно описать вокруг прямой призмы, если ее основанием является многоугольник, вокруг которого можно описать окружность. При этом радиус цилиндра R равен радиусу этого круга.

2) Высота Н призмы, которая соединяет центры окружностей, описанных вокруг основ, принадлежит оси цилиндра.

Пример. Можно описать цилиндр вокруг прямой призмы, в основании которой лежит: 1) треугольник, 2) ромб, который не является квадратом?

Решения. 1) Да, поскольку вокруг любого треугольника можно описать окружность.

2) Нет, поскольку вокруг ромба, который не является квадратом, нельзя описать окружность.