ГЕОМЕТРИЯ

Раздел ІІ. СТЕРЕОМЕТРИЯ

§22. ШАР. СФЕРА.

4. Сечение шара плоскостью.

Если плоскость α и пуля лежат множество общих точек (рис. 503), то говорят о сечении шара плоскостью.

Если плоскость проходит через центр шара (рис. 500), то ее называют диаметральной плоскостью. Сечение шара диаметральной плоскостью есть круг, радиус которого равен радиусу шара. Такое сечение называют большим кругом, а круг, что его ограничивает - большим кругом.

Сечение шара плоскостью, отличной от диаметральной плоскости, есть также круг, радиус которого меньше радиуса шара. На рисунке 500 сечением шара плоскостью α есть круг, центр которого - точка А, которая является основанием перпендикуляра, опущенного из центра шара - точки О на плоскость α. Радиус этого круга АМ, где М - точка, принадлежащая плоскости сечения α со сферой, ограничивающей шар. При этом ОМ = r - радиус шара.

Пример. Диаметр шара равен 50 см. Шар пересечена плоскостью на расстоянии 24 см от центра. Найти площадь образованного сечения.

Решения. 1) Радиус шара r = 50 : 2 = 25 (см).

2) По рисунку 503: 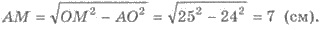АМ - радиус сечения.

3) Площадь сечения