ГЕОМЕТРИЯ

Раздел ІІ. СТЕРЕОМЕТРИЯ

§22. ШАР. СФЕРА.

2. Взаимное расположение шара и плоскости.

Плоскость α и пуля могут либо не иметь общих точек (рис. 501) или иметь одну общую точку (рис. 502) или пересекаться и иметь множество общих точек (рис. 503).

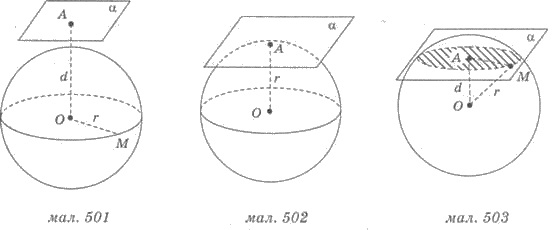
Пусть ОМ = r - радиус шара, а О А = d - перпендикуляр, опущенный из центра шара - точка О к плоскости α (расстояние от центра шара до плоскости α).

а) Если плоскость α и пуля не имеют общих точек, то d > r;

б) Если плоскость α и шар имеют одну общую точку, то d = r;

в) Если плоскость α и шар имеют множество общих точек, то d r.

Заметим, что обратное утверждение также верно: если d > r, то плоскость и шар не имеют общих точек, если d = r, то плоскость и шар имеют одну общую точку, если d r, то плоскость и шар имеют множество общих точек.

Пример. Радиус шара равен 4,5 см. Сколько общих точек имеет шар с плоскостью, если расстояние от центра шара к плоскости равен: 1) 4 см 2) 4(1/2) см 3) 5 см.

Решения. 1) 4 4,5, поэтому множество общих точек.

2) 4(1/2) = 4,5, поэтому одна общая точка.

3) 5 > 4, поэтому ни одной общей точки.

Рассмотрим подробнее случаи, когда плоскость и шар имеют одну или множество общих точек.