УРОК № 53
Тема. Взаимное расположение прямой и плоскости и плоскостей в пространстве. Перпендикуляр к плоскости. Взаимное расположение плоскостей в пространстве
Цель урока: повторить, привести в систему и расширить сведения о плоскость и взаимное расположение двух плоскостей в пространстве; познакомить учащихся с различными случаями взаимного расположения прямой и плоскости; дать представление о перпендикуляр к плоскости.
Тип урока: комбинированный.
Наглядность и оборудование: таблица «Начальные сведения стереометрии» [13].
Требования к уровню подготовки учащихся: описывают взаимное расположение в пространстве прямой и плоскости, двух плоскостей, применяют изученные определения и свойства к решению задач.
Ход урока
И. Проверка домашнего задания
Проверить выполнение домашнего задания с записями, сделанными на доске до начала урока.
Дано: АВ С АВ (рис. 229).
АВ (рис. 229).
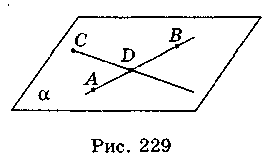
Докажите: прямая АВ и точка С лежат в плоскости α.
Доведение
Возьмем точку D, которая лежит на прямой АВ. Проведем прямую CD. Через прямые АВ и CD, которые пересекаются, проводим плоскость α. Что и требовалось доказать.
Фронтальная беседа
- 1) Что изучает стереометрия?
- 2) Назовите основные геометрические фигуры стереометрии.
- 3) Сформулируйте аксиомы стереометрии.
- 4) Каково взаимное расположение двух прямых в пространстве возможно?
- 5) Сколько различных плоскостей можно провести через:
а) три точки, не лежащие на одной прямой;
б) три точки; которые лежат на одной прямой;
в) прямую и точку, не принадлежащую этой прямой?
II. Поэтапное восприятие и осознание нового материала
Взаимное расположение двух плоскостей
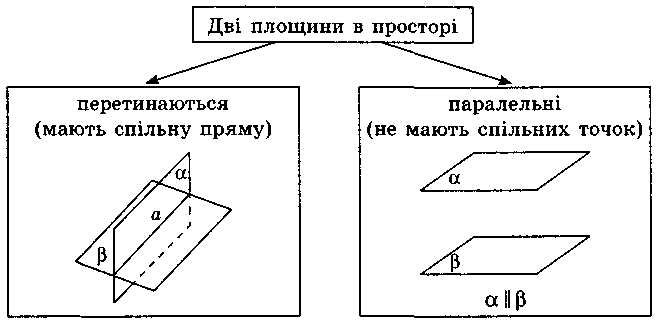
Мы знаем, что если две различные плоскости имеют общую точку, то они пересекаются по прямой, которая проходит через эту точку. Это утверждение - аксиома стереометрии. Отсюда следует, что две плоскости либо пересекаются по прямой, или не пересекаются, т.е. не имеют общих точек (рис. 230).
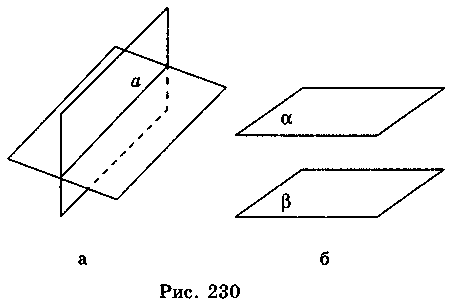
Две плоскости называются параллельными, если они не пересекаются.
Представление о параллельных плоскости дают пол и потолок классной комнаты, две противоположные стены классной комнаты, поверхность стола и плоскость пола.
Если плоскости α и β параллельны, то пишут: α || β.
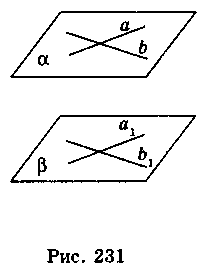
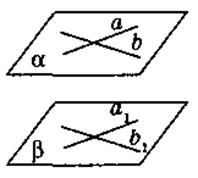
Две плоскости будут параллельны, если две прямые, лежащие в одной плоскости и пересекаются, параллельны двум прямым другой плоскости (рис. 231), т.е. если a || a1, b || b1, то α || β. Доказательства этого утверждения мы опускаем.
Задача класса
- 1. Приведите примеры параллельных плоскостей из окружения.
- 2. На моделях куба, прямоугольного параллелепипеда покажите параллельные плоскости и плоскости, которые пересекаются.
- 3. Пользуясь изображением прямоугольного параллелепипеда ABCDA1B1C1D1 (см. рис. 223), укажите:
а) грани, которые пересекают грань ABCD;
б) плоскости, параллельные плоскости ABC.
- 4. Дано: куб ABCDA1B1C1D1. Докажите параллельность плоскостей:
а) АВС и A1B1C1; б) AB1D1 и BDC1.
В ходе объяснения нового материала учащиеся составляют конспект (табл. 8).
Таблица 8
Взаимное расположение двух плоскостей |
|
|
Если а и b пересекаются и лежат в плоскости α, а1 || а, b1 || b, а прямые а1 || b1 лежат в плоскости β, то α || β |
Плоскость и прямая, не лежащая в плоскости, либо не пересекаются, либо пересекаются в одной точке.
Случаи взаимного расположения прямой и плоскости
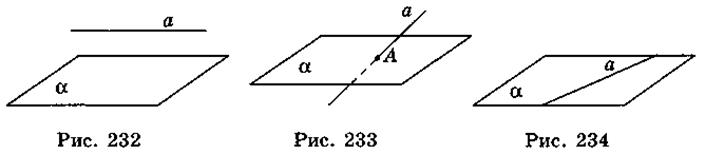
- 1. Плоскость α не имеет общих точек с прямой а. Прямая и плоскость, которые не имеют общих точек, называются параллельными, обозначаются а || α (рис. 232).
- 2. Плоскость α имеет с прямой а только одну общую точку. В этом случае говорят, что прямая а и плоскость α (рис. 233) пересекаются.
- 3. Прямая а лежит в плоскости α (рис. 234).
Прямая называется перпендикулярной к плоскости, если она пересекает эту плоскость и перпендикулярна к любой прямой, лежащей в этой плоскости и проходит через точку пересечения.
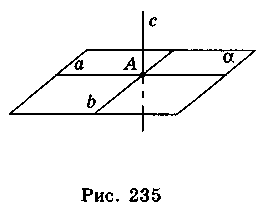
На рис. 235 прямая с перпендикулярна к плоскости α. Пишут: c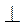 α. Из определения следует, что с
α. Из определения следует, что с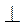 a, с
a, с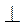 b, ... .
b, ... .
Представление о прямую, перпендикулярную к плоскости, дают вертикальные столбы - они перпендикулярны к поверхности земли, перпендикулярные к любой прямой, проходящей через основание столба и лежит в плоскости земли.
Как проверить, перпендикулярна данная прямая в данной плоскости? Этот вопрос имеет практическое значение, например, при установке мачт, колонн и т.п., которые нужно устанавливать вертикально, то есть перпендикулярно к плоскости земли. На самом деле нет необходимости проверять перпендикулярность прямой до всех прямых, лежащих в данной плоскости и проходят через точку пересечения данной прямой и плоскости. Достаточно проверить перпендикулярность лишь двух прямых, лежащих в плоскости и проходят через точку пересечения прямой и плоскости. Справедлива такая теорема:
Если прямая перпендикулярна к двум прямым, которые пересекаются и лежат в плоскости, то данная прямая перпендикулярна к плоскости.
Доказательство этой теоремы мы не приводим.
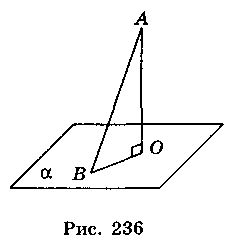
Перпендикуляром к плоскости называется отрезок прямой, перпендикулярной к плоскости, что содержится между данной точкой прямой и точкой пересечения ее с плоскостью.
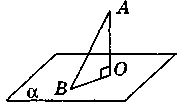
На рис. 236 АО - перпендикуляр к плоскости. Любой другой отрезок, соединяющий точку А с произвольной точкой В плоскости α, называется наклонной. Отрезок ВО называют проекцией наклонной АВ на плоскость α.
Выполнение упражнений
- 1. На предметах окружающей среды покажите различные случаи взаимного расположения прямой и плоскости.
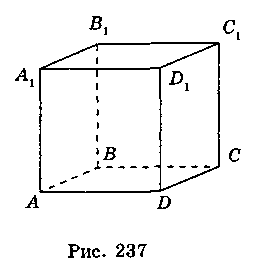
- 2. Определите взаимное расположение плоскости ABC (используя изображение куба ABCDA1B1C1D1 на рис. 237) и прямых:
a) CD; б) АС1; в) B1D; г) DС1; д) D1С1; В1D1.
- 3. Укажите в окружающей среде модели перпендикулярных прямых и плоскостей.
- 4. Правильно ли, что если прямая не перпендикулярна к плоскости, то она перпендикулярна ко всякой прямой, лежащей в этой плоскости?
- 5. Как вы понимаете утверждение: прямая не перпендикулярна к плоскости?
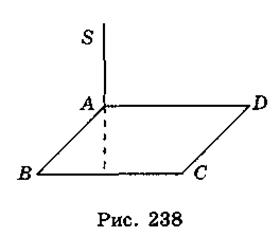
- 6. Прямая SA перпендикулярна к плоскости прямоугольника ABCD (рис. 238). Укажите перпендикулярные прямые.
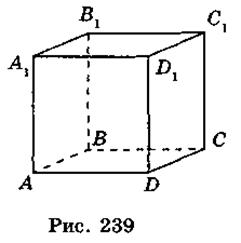
- 7. Дано изображение куба ABCDA1B1C1D1 (рис. 239). Докажите, что:
а) прямая АА1 и перпендикулярна к плоскости ABC;
б) прямая AD перпендикулярна к плоскости DCC1;
в) прямая B1D1 перпендикулярна к плоскости A1C1C;
г) прямая A1B1 перпендикулярна к прямой BC1.
д) треугольник AB1C1 прямоугольный.
есть) четырехугольник AB1C1D1 - прямоугольник.
- 8. Найдите длину наклонной, если длина перпендикуляра равна 4 см, а проекция наклонной на плоскость - 3 см.
- 9. Найдите проекцию наклонной на плоскость, если наклонная равна 13 см, а перпендикуляр, проведенный из этой точки, - 12 см.
- 10. Найдите длину перпендикуляра, если наклонная равна 10 см, а проекция наклонной на плоскость - 8 см. В табл. 9 приведен образец конспекта урока.
III. Закрепление и осмысление нового материала
Решение задач
- 1. Две прямые одной плоскости параллельны двум прямым другой плоскости. Правильно, что такие плоскости всегда параллельны? Воспользуйтесь моделями.
- 2. Докажите, что параллельные плоскости пересекаются секущей плоскостью по параллельным прямым.
Доведение
Пусть в плоскость пересекает параллельные плоскости α и β по прямым а и b (рис. 240). Докажем, что а || b.
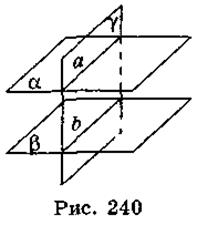
Предположим, что прямые а и b имеют общую точку, то эта точка - общая для плоскостей α и β. Но этого не может быть, потому что данные плоскости α и β параллельны. Итак, прямые а и b не могут пересекаться, а поскольку они лежат в одной плоскости, то а || b.
- 3. Постройте изображение прямоугольного параллелепипеда ABCDA1B1C1D1. Укажите:
а) грани, перпендикулярные к ребру АА1; АВ; В1C1;
б) ребра, перпендикулярные грани DCC1D1.
- 4. Укажите, какие из приведенных утверждений являются правильными, а какие - неправильные.
- 1) Прямая перпендикулярна к плоскости, если она перпендикулярна к двум различным прямым этой плоскости.
- 2) Две прямые, перпендикулярные к одной и той же прямой, параллельны.
- 5. Как на практике можно проверить вертикальность установленного столба?
- 6. Как с помощью уровня можно проверить горизонтальность установленной подставки для прибора?
- 7. Концы отрезка, не пересекающего плоскость, удалены от нее на 10 см и 20 см. Найдите расстояние от плоскости до середины отрезка.
- 8. Ребро куба равно а. Найдите расстояние от одной из вершин куба до других его вершин.
IV. Домашнее задание
- 1. Изучить материал о взаимное расположение прямой и плоскости и плоскостей в пространстве.
- 2. Решить задачи.
- 1) Измерения прямоугольного параллелепипеда равны 1 см, 2 см, 2 см. Найдите расстояние от одной из вершин прямоугольного параллелепипеда до других его вершин.
- 2) Докажите, что параллельные плоскости отсекают от параллельных прямых равные отрезки.
V. Подведение итогов урока
Задача класса
Определите, какие из приведенных утверждений являются правильными, а какие-неправильными.
- 1. Если α || β, то любая прямая плоскости α не имеет общих точек с плоскостью β.
- 2. Если α || β, то любая прямая плоскости α параллельна каждой прямой плоскости β.
- 3. Если α || β, то любая прямая плоскости α мимобіжна каждой прямой плоскости β.
- 4. Если α || β, то для любой прямой а в плоскости α существует прямая b в плоскости β такая, что a || b.
- 5. Если α || β, то прямая, которая пересекает плоскость α, и пересекает плоскость β.
V. Подведение итогов урока
Вопрос к классу
- 1. Какая прямая называется параллельной плоскости?
- 2. Какая прямая называется перпендикулярной к плоскости?
- 3. Что такое перпендикуляр? наклонная?
Таблица 9
Взаимное расположение прямой и плоскости |
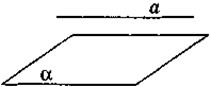
|
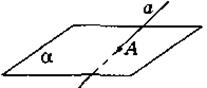
|
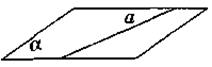
|
параллельные a || α |
пересекаются |
прямая лежит в плоскости |
Прямая, перпендикулярная к плоскости |
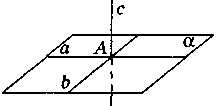
|
Определение. Прямая перпендикулярна к плоскости α, если c 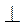 a, c a, c 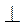 b , .. b , ..
Теорема. Если с 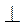 а, c а, c 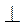 b , то с b , то с  α α |
Перпендикуляр и наклонная |
|
АО - перпендикуляр,
АВ - наклонная,
ВО - проекция наклонной АВ на плоскость α |
















