УРОК № 52
Тема. Взаимное расположение прямых в пространстве
Цель урока: повторить, привести в систему и расширить сведения о взаимное расположение двух прямых в пространстве.
Тип урока: комбинированный.
Наглядность и оборудование: таблица «Начальные сведения стереометрии» [13].
Требования к уровню подготовки учащихся: описывают взаимное расположение в пространстве двух прямых; применяют изученные определения и свойства к решению задач.
Ход урока
I. Проверка домашнего задания
Проверить наличие выполненных домашних заданий и ответить на вопросы учащихся, возникшие при их решении.
В конце урока собрать рабочие тетради для проверки домашнего задания и выставления оценок за ведение тетрадей.
II. Анализ результатов контрольной работы
- 1. Объявить статистические данные о баллах, что получили ученики.
- 2. Опираясь на анализ контрольной работы, сообщить ученикам о типичных ошибках, допущенных в контрольной работе. После этого учащиеся работают над ошибками, которые они допустили при написании контрольной работы.
- 3. Для учеников, которые полностью справились с тематической контрольной работой, можно предложить задачи повышенной сложности.
III. Мотивация учебной деятельности
Вы ознакомились с планіметрією. Планиметрия - это раздел геометрии, в котором изучают свойства плоских геометрических фигур: треугольников, параллелограммов, окружностей и т.д.
Но, кроме плоских фигур, существуют и пространственные фигуры: прямоугольный параллелепипед, куб, пирамида, цилиндр, конус, шар. Многие предметы, которые нас окружают, имеют форму прямоугольного параллелепипеда: классная комната, кирпич, спичечная коробка и т.д. Популярная во всем мире игрушка - кубик Рубика - имеет форму куба.
Хорошо известные пирамиды Древнего Египта дают нам представление о широкий класс геометрических тел, которые называются пирамидами.
IV. Поэтапное восприятие и осознание нового материала
Пространственные геометрические фигуры
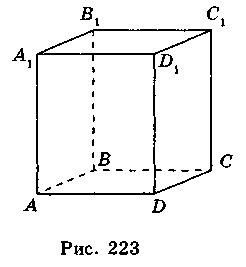
Прямоугольный параллелепипед - это пространственная геометрическая фигура, которая ограничена шестью прямоугольниками, которые называются гранями. Стороны прямоугольников называются ребрами прямоугольного .паралелепіпед а, а вершины прямоугольников - вершинами прямоугольного параллелепипеда (рис. 223).
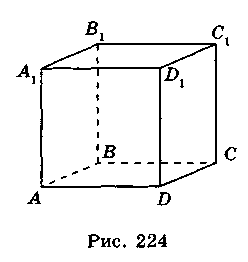
Куб - это прямоугольный параллелепипед, у которого все шесть граней - квадраты (рис. 224).
Прямоугольный параллелепипед и куб - это представители большого класса геометрических фигур, которые называют многогранниками. Кроме многогранников в геометрии рассматривают и другие пространственные фигуры: цилиндры, конусы, шары и т.п.
Раздел геометрии, в котором изучаются свойства пространственных фигур, называется стереометрією.
Верхнюю и нижнюю грани прямоугольного параллелепипеда называют основами, а ребра этих граней - ребрами основания, другие ребра называют боковыми ребрами, а остальные грани - боковыми гранями.
Задача класса
- 1. Назовите боковые грани и боковые ребра прямоугольного параллелепипеда (см. рис. 223).
- 2. Назовите переднюю, заднюю, левую, правую, верхнюю, нижнюю грани куба (рис. 224).
- 3. Назовите основания и ребра основания куба (рис. 224).
Основные пространственные фигуры
Основными фигурами пространства есть точка, пряжа и плоскость.
Представление о точки и прямые вы имеете из курса планиметрии. Напомним, что точки обозначают большими латинскими буквами, например: А, В, С, ...; прямые обозначают малыми латинскими буквами, например: прямые а, Ь, с, ..., или двумя заглавными буквами, например: прямые АВ, ВС, CD, ... . Материальными моделями части плоскости, например, поверхность стола, поверхность оконного стекла, мраморная плита и т.д.
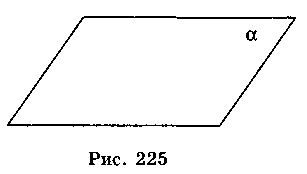
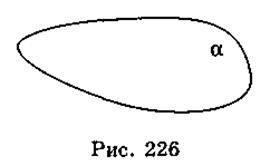
В геометрии плоскость представляют неограниченной, идеально ровной и гладкой. Изображающие плоскость в виде параллелограмма (рис. 225) или в виде произвольной области (рис. 226). Обозначаются плоскости маленькими греческими буквами, например: плоскости α, β, γ, ... .
Как и любая геометрическая фигура, плоскость состоит из точек. Если точка А лежит в плоскости α, то говорят, что плоскость α проходит через точку А, и записывают так: А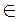 α. Если точка А не лежит на плоскости α, говорят, что плоскость α, не проходящей через точку А, и записывают так: А
α. Если точка А не лежит на плоскости α, говорят, что плоскость α, не проходящей через точку А, и записывают так: А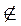 α.
α.
Если каждая точка прямой а лежит в плоскости α, говорят, что прямая лежит в плоскости α или плоскость α проходит через прямую а, и записывают так: a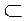 α; a
α; a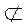 α.
α.
Задача класса
Постройте и запишите с помощью символов:
а) плоскость α и точка А, которая лежит в ней;
б) плоскость β и точку В, которая не принадлежит ей;
в) плоскость γ, проходящая через прямую а;
г) плоскость α и прямая а, не лежащая в плоскости α;
д) две плоскости β и γ, которые проходят через прямую с.
Основные аксиомы стереометрии
Как и в планиметрии, свойства основных фигур в стереометрии выражаются аксиомами.
Напомним, что в планиметрии свойство прямых и точек выражалась аксиомой:
Какова бы не была прямая, существуют точки, принадлежащие этой прямой, и точки, ей не принадлежащие. Через две различные точки можно провести прямую и к тому же только одну.
Взяв какую-либо плоскость (например, плоскость пола классной комнаты), мы можем указать точки, принадлежащие этой плоскости, и точки, не принадлежащие ей. Поэтому одно из свойств плоскости в пространстве выражается аксиомой.
Аксиома 1. Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, ей не принадлежащие.
Аксиома 2. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
Наглядной иллюстрацией аксиомы 2 является пересечение двух стен, стены и пола классной комнаты.
Аксиома 3. Если две различные прямые имеют общую точку, то через них можно провести плоскость и только одну.
Никаких инструментов, которыми бы можно было построить в пространстве плоскость, нет. Поэтому выражение «можно провести плоскость» употребляется в значении «существует плоскость».
Единую плоскость можно провести:
- 1) через две прямые, которые пересекаются;
- 2) через две параллельные прямые;
- 3) через прямую и точку, которая не лежит на этой прямой;
- 4) через три точки, не лежащие на одной прямой.
Следует отметить, что в пространстве существует множество плоскостей, для каждой плоскости справедливы все аксиомы и теоремы планиметрии. Более того, признаки равенства и подобия треугольников справедливы и для треугольников, лежащие в разных плоскостях.
Задача класса
- 1. Назовите вершины, ребра, грани прямоугольного параллелепипеда (см. рис. 223).
- 2. Пользуясь изображением куба (см. рис. 224), укажите точки, которые:
а) не относятся передней грани;
б) принадлежат верхней грани;
в) принадлежат грани ABCD;
г) не принадлежат грани А1В1ВА.
- 3. Пользуясь рис. 223, укажите:
а) общие точки верхней и передней граней;
б) прямую пересечения задней и нижней граней;
в) общие точки плоскостей граней АВВ1А1 и А1В1С1D1;
г) прямую пересечения граней A1B1C1D1 и ВВ1С1С.
- 4. Пользуясь рис. 223, укажите какую плоскость определяют прямые:
а) АВ и AD; б) ВС и СС1; в) DC и СС1; г) А1B1 и В1А.
- 5. Пользуясь изображением куба на рис. 224, докажите, что можно провести плоскость через прямые:
а) АС и СС1; б) AD и DC1.
Взаимное расположение двух прямых в пространстве
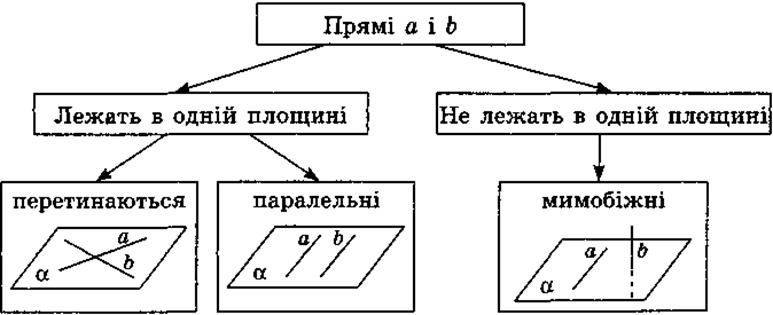
Из планиметрии известно, что две прямые, лежащие в плоскости, могут пересекаться или не иметь общих точек. Если две прямые лежат в одной плоскости и не имеют общих точек, то они называются параллельными. В пространстве две различные прямые либо пересекаются, либо не пересекаются. Однако второй случай допускает две возможности: прямые лежат в одной плоскости или прямые не лежат в одной плоскости.
Прямые, которые не пересекаются и лежат в одной плоскости, называются параллельными.
Прямые, которые не пересекаются и не лежат в одной плоскости, называются скрещивающимися.
(Случаи взаимного расположения двух прямых в пространстве демонстрируются с помощью стереометричного ящика или на каркасной модели куба.)
Итак, две прямые а и b в пространстве могут пересекаться, быть параллельными, быть скрещивающимися.
Задача класса
- 1. Продемонстрируйте различные случаи расположения двух прямых в пространстве на предметах окружения.
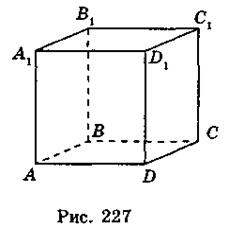
- 2. Дано изображение куба ABCDA1B1C1D1 (рис. 227).
а) пересекаются Ли прямые АА1 и BB1? A1В1 и D1С1? Как называются эти прямые?
б) пересекаются Ли прямые AD иB1? АВ и DD1? Как называются эти прямые?
в) можно Ли провести плоскость через прямые: AD и DB1? A1D1 и C1D1? AD и BB1? АA1 и DB1? АА1 и DD1?
V. Закрепление и осмысление нового материала
Решение задач
- 1. Докажите, что через три точки, не лежащие на одной прямой, можно провести плоскость.
Доведение
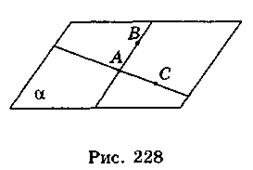
Пусть А, В, С - три данные точки, которые не лежат на одной прямой (рис. 228). Проведем прямые АВ и АС: они разные, потому что точки А, В, С не лежат на одной прямой. По аксиоме стереометрии через прямые АВ и АС, которые пересекаются, можно провести плоскость α. Что и требовалось доказать.
- 2. Прямые АВ и CD не лежат в одной плоскости. Докажите, что прямые АС и BD не могут пересекаться.
Доведение
Если предположить, что прямые АС и BD пересекаются, то они лежат в некоторой плоскости. Тогда все точки А, В, С, D лежат в этой плоскости, а следовательно, и прямые АВ и CD лежат в одной плоскости, что противоречит условию. Таким образом, прямые АС и BD не могут пересекаться.
VI. Домашнее задание
- 1. Изучить материал о взаимное расположение прямых в пространстве.
- 2. Решить задачу.
Докажите, что через прямую и точку, которая ей не принадлежит, можно провести плоскость.
VII. Подведение итогов урока
Вопрос к классу
- 1. Какие две прямые называются параллельными?
- 2. Какие две прямые называются скрещивающимися? Приводим образец конспекта (табл. 7).
Таблица 7
Стереометрия-раздел геометрии, изучающий свойства пространственных фигур |
Основные геометрические фигуры |
Рисунок |
Фигуры |
Обозначения |
|
Точки |
А, В, С, ... |
|
Прямые |
а, b, с, ... АВ, ВС, ... |
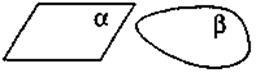
|
Плоскости |
α, β, γ. ... |
Аксиомы стереометрии |
|
|
|
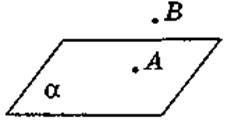
Какова бы ни была плоскость, существуют точки, принадлежащие ей, и точки, ей не принадлежащие |
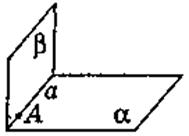
Если две плоскости имеют общую точку, то они пересекаются по прямой, которая проходит через эту точку |
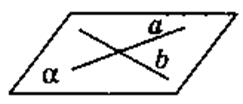
Через две прямые, которые пересекаются, можно провести плоскость, и только одну |
Взаимное расположение двух прямых в пространстве |
|