УРОК № 53

Тема. Сумма первых n членов арифметической прогрессии

Цель урока: закрепить знания учащихся о формулах вычисления суммы первых n членов арифметической прогрессии, а также о ее определения и свойства, изученные на предыдущих уроках; сформировать представление о способе решения задач на отыскание суммы последовательных членов арифметической прогрессии с n-го по т-й включительно (n m).

Закрепить умения: записывать изученные формулы в соответствии с данными задачи, а также применять их как в стандартных ситуациях (с использованием понятия суммы первых n членов арифметической прогрессии), так и в нестандартных ситуациях (для поиска суммы последовательных членов арифметической прогрессии с n-го по m-й включительно, n m.)

Тип урока: дополнение знаний, закрепления знаний, отработки умений и навыков.

Наглядность и оборудование: опорный конспект № 32.

Ход урока

I. Организационный этап

Учитель проверяет готовность учащихся к уроку, настраивает их на работу.

II. Проверка домашнего задания

Для осознанной работы учащихся на этом этапе урока можно провести проверку выполнения домашнего задания по образцу.

Другой вариант проведения этого этапа урока - математический диктант (см. ниже) с последующей проверкой и обсуждением результатов его написания, во время которых повторяется содержание основных понятий предыдущего урока, а также схемы применения изученных на этом уроке понятий для решения типовых задач.

Математический диктант

1. В арифметической прогрессии (аn) а1 = 1, d = 4. Найдите а10, S10.

2. Дано арифметической прогрессии (аn). Найдите:

1) n, если a1 = 5, an = 25, Sn = 150;

2) a1, если d = 2, n = 4, S4 = 10.

3. Выразите из формулы :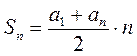

1) a1; 2) аn.

III. Формулировка цели и задач урока.

Мотивация учебной деятельности учащихся

Основная цель урока формулируется после выполнения работы, предложенной на предыдущем этапе урока с учетом результатов ее выполнения: при большом количестве ошибок и низком уровне выполнения работы проводится закрепление знаний и умений, сформированных на предыдущем уроке; если результаты выполнения работы удовлетворительные, то акцент перемещается на совершенствование знаний и умений, а следовательно, на выработку определенных умений применять приобретенные знания и умения в нестандартных ситуациях.

IV. Актуализация опорных знаний и умений учащихся

Устные упражнения

1. Найдите разность арифметической прогрессии, у которой первый член 4, а второй 6.

2. Найдите третий член арифметической прогрессии, если ее первый член 6, а второй 4.

3. Найдите десятый член арифметической прогрессии, если ее первый член 1, а разность 4.

4. Есть ли последовательность четных натуральных чисел арифметической прогрессией?

5. Найдите сумму первых пяти членов арифметической прогрессии, если ее первый член 5, пятый 6.

6. Найдите сумму первых пяти членов арифметической прогрессии, если ее первый член - 20, а разница 10.

7. Сколько членов арифметической прогрессии стоит перед 2-м, 5-м, 20-м, п-м членом этой прогрессии?

V. Дополнение знаний учащихся

Опорный конспект № 32

Методический комментарий

Единственный новый момент, который прилагается к изученных на предыдущем уроке формул суммы первых n членов арифметической прогрессии и способов их применения при решении задач, - это использование изученных формул при решении задач на отыскание суммы последовательных членов арифметической прогрессии с n-го по m-й включительно (n m).

Формирование представления о один из способов решения таких задач основывается на определении числовой последовательности как функции, заданной на множестве натуральных чисел, а также на известных учащимся с 5 класса свойствах натурального ряда. Второй способ решения таких задач основан на свойствах самой арифметической прогрессии: последовательные члены арифметической прогрессии, начиная с любого ее члена, образуют арифметическую прогрессию. Это свойство можно было рассмотреть на предыдущем уроке при изучении свойств арифметической прогрессии (см. опорный конспект № 32).

VI. Отработка умений

Письменные упражнения

Содержание письменных упражнений урока может быть таким:

1) задачи на отыскание суммы последовательных членов арифметической прогрессии с n-го по m-й включительно (n m) и задачи, сводящиеся к этому;

2) задачи на применение изученных формул для отыскания неизвестных первого члена, или разницы или числа n членов арифметической прогрессии с известным по условию суммой ее первых членов;

3) прикладные задачи на применение изученных на предыдущих четырех уроках формулам для арифметической прогрессии.

Методический комментарий

Содержание упражнений и цель их решения такие же, как и на предыдущем уроке: закрепление формул, изученных на этих уроках, а также выработки оперативных умений применения формул при решении задач в различных ситуациях (если позволяют успехи учащихся, повышается уровень сложности задач за счет задач на применение свойств арифметической прогрессии).

VII. Итоги урока

Контрольные вопросы

Опишите последовательность действий при решении задачи (в задачах 1 - 6 (аn) - арифметическая прогрессия):

1) дано: а1, а2. Найти d;

2) дано: а1, а2. Найти а3;

3) дано: а1, d. Найти а10;

4) дано: а1, а10. Найти S10;

5) дано: al, d. Найти S10;

6) дано: а1 и а2. Найти сумму с 4-го по 10-й члены включительно.

VIII. Домашнее задание

1. Изучить содержание материала в опорных конспектах № 31, 32.

2. Решить самостоятельную работу (см. ниже) с вариантом, указанным учителем.

Самостоятельная работа

Вариант 1

Найдите сумму:

1) первых шестнадцати членов арифметической прогрессии, если ее первый и шестнадцатый члены соответственно равны 3 и -5;

2) первых шестнадцати членов арифметической прогрессии, если ее первый член равен 6, а разница 3;

3) первых сорока семи членов арифметической прогрессии, заданной формулой общего члена ап = 3n - 1;

4) членов арифметической прогрессии с 6-го по 23-й включительно, если первый член равен 28, а пятый равен 16.

Вариант 2

Найдите сумму:

1) первых восемнадцати членов арифметической прогрессии, если ее первый и восемнадцатый члены соответственно равны 3,8 и -5;

2) первых восемнадцати членов арифметической прогрессии, если ее первый член равен 2,4, а разница -0,3;

3) первых тридцати восьми членов арифметической прогрессии, заданной формулой общего члена аn = -2n + 1;

4) членов арифметической прогрессии с 7-го по 26-й включительно, если второй член равен 37, а шестой равен 29.