ГЕОМЕТРИЯ

Раздел ІІ. СТЕРЕОМЕТРИЯ

§20. КОНУС.

2. Сечения конуса плоскостями.

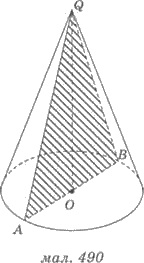
Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением (рис. 490). Осевой сечение конуса - равнобедренный треугольник, основание которого - диаметр конуса, а боковые стороны - образующие конуса. Высоты равнобедренного треугольника совпадает с высотой конуса. На рисунке 490 треугольник QАВ - осевое сечение конуса, АВ - диаметр конуса, QА и QВ - образующие конуса, QО - высота конуса.

Если осевым сечением конуса является равносторонний треугольник, его иногда называют равносторонним (или равносторонним или равнобедренным).

Пример 1. Длина окружности основания конуса равна 4π см. Найти площадь осевого сечения конуса, если он является прямоугольным треугольником.

Решения. 1) Пусть QАВ - осевое сечение конуса, BQA = 90° (рис. 490).

2) Обозначим ОВ = ОА = r. По условию 2πr = 4π, тогда r = 2 см.

3) ∆QАВ - равнобедренный прямоугольный:

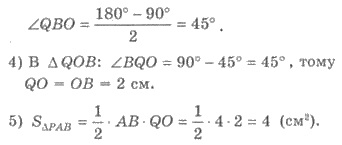
Сечение конуса плоскостью, которая является параллельной плоскости основания является круг (рис. 491). Центр этого круга - точка О находится на оси конуса.

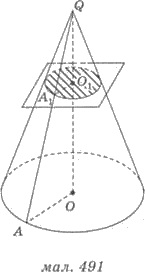
Пример 2. Высота конуса равна 9 см, а радиус основания - 6 см. На расстоянии 3 см от вершины конуса проведено сечение плоскостью, параллельной основанию конуса. Найти площадь этого сечения.

Решения. 1) По условию задачи OQ = 9 см, АО = 6 см, QО₁ = 3 см (рис. 491).

2) ∆QА₁O₁ ∆QАО (по двум углам), тогда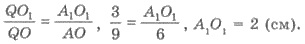

3) Тогда площадь сечения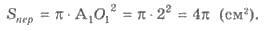

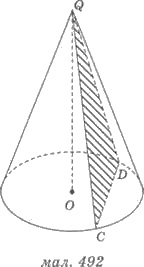
Сечением конуса плоскостью, проходит через вершину конуса является равнобедренный треугольник, боковыми сторонами которого есть образующие конуса. На рисунке 492 треугольник QСD - сечение конуса плоскостью, проходящей через вершину конуса Q. Его боковые стороны - образующие QС и QD конуса, а основание - хорда основания конуса СD.

Пример 3. Через вершину конуса проведено сечение, который наклонен к плоскости основания под углом 60°. Найти высоту конуса, если расстояние от центра основания хорды, по которой сечение пересекает основание, равна 4 см.

Решения. 1) Пусть QСD - сечение, о котором идет речь в задаче (рис. 493).

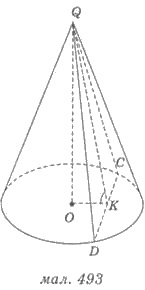
2) ∆QСD - равнобедренный, СD - его основа, проведем QК - высоту и медиану ∆QСD.

3) Поскольку QК СD и ОК - проекция QК на плоскость основания, то по теореме о трех перпендикуляры, получим ОК СD.

4) Тогда ОК - расстояние от точки О до хорды СD, ОК = 4 см (по условием).

5) Поскольку QК СD и ОК СD, то плоскость DQК перпендикулярна хорде СD, поэтому QКО - угол наклона сечения QСD до плоскости основы. По условию QКО = 60°.