УРОК № 51
Тема. Тематическая контрольная работа № 5
Цель урока: контроль учебных достижений учащихся по цели «Векторы».
Тип урока: комбинированный.
Требования к уровню подготовки учащихся: применяют определения и свойства геометрических фигур при решении задач.
Ход урока
И. Тематическое оценивание № 5
Тематическое оценивание № 5 можно провести в виде тематической контрольной работы.
Приводим текст контрольной работы. Каждый правильный ответ оценивается в 3 балла.
Вариант 1
- 1. Найдите координаты вектора
 =
=  - 2
- 2 , если
, если  (1; 1),
(1; 1),  (3; 1).
(3; 1).
- 2. Даны три вершины параллелограмма ABCD: A(-2; 1), В(-1; 1), С(1; 1). Найдите координаты вершины D.
- 3. Даны векторы
 (4; 2) и
(4; 2) и  (x; -4). При каком значении х эти векторы коллинеарны?
(x; -4). При каком значении х эти векторы коллинеарны?
- 4. Треугольник ABC задан координатами его вершин: А(-1; 1), В(0; 2), С(1; 1). Найдите внешний угол при вершине А.
Вариант 2
- 1. Найдите координаты вектора
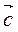 = 2
= 2 -
-  , если
, если  (1; 1),
(1; 1),  (3; 1).
(3; 1).
- 2. Даны три вершины параллелограмма ABCD: A(1; -3), В(2; -1), D(3; -3). Найдите координаты вершины С.
- 3. Даны векторы
 (4; 2) и
(4; 2) и  (x; -4). При каком значении х эти векторы перпендикулярны?
(x; -4). При каком значении х эти векторы перпендикулярны?
- 4. Треугольник ABC задан координатами его вершин: А(3; 5), В(4; 6), С(5; 5). Найдите внешний угол при вершине А.
Вариант 3
- 1. Найдите координаты вектора
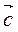 =
=  - 3
- 3 , если
, если  (-1; 2),
(-1; 2),  (1; -2).
(1; -2).
- 2. Даны три вершины параллелограмма ABCD: A(-4; 1), В(-1; 3), D(-2; 1). Найдите координаты вершины С.
- 3. Даны векторы
 (2; 5) и
(2; 5) и  (-6; в). При каком значении в эти векторы перпендикулярны?
(-6; в). При каком значении в эти векторы перпендикулярны?
- 4. Треугольник ABC задан координатами его вершин: А(1; 3), В(2; 4), С(3; 3). Найдите внешний угол при вершине А.
Вариант 4
- 1. Найдите координаты вектора
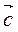 = 3
= 3 -
-  , если
, если  (-1; 2),
(-1; 2),  (1; -2).
(1; -2).
- 2. Даны три вершины параллелограмма ABCD: В(1; 3), С(-1;4), D(-2;2). Найдите координаты вершины А.
- 3. Даны векторы
 (2; 5) и
(2; 5) и  (-6; в). При каком значении в эти векторы коллинеарны?
(-6; в). При каком значении в эти векторы коллинеарны?
- 4. Треугольник ABC задан координатами его вершин: А(0; 2), В(1; 3), С(2; 2). Найдите внешний угол при вершине А.
Ответы и решения к заданиям тематической контрольной работы
Вариант 1
1. 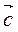 (1 - 2 ∙ 3; 1 - 2 ∙ 1) =
(1 - 2 ∙ 3; 1 - 2 ∙ 1) = 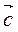 (-5; -1). Ответ.
(-5; -1). Ответ. 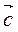 (-5; -1).
(-5; -1).
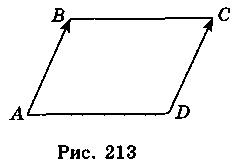
2. Пусть D(x; y), тогда 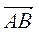 (1; 0),
(1; 0), 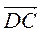 (1 - x; 1 - в) (рис. 213). Поскольку
(1 - x; 1 - в) (рис. 213). Поскольку 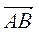 =
= 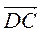 , то
, то 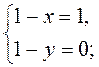
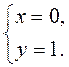 Следовательно, D(0; 1). Ответ. D(0; 1).
Следовательно, D(0; 1). Ответ. D(0; 1).
3. Векторы коллинеарны, если 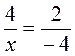 , тогда х = -16, х = -8. Ответ. х = -8.
, тогда х = -16, х = -8. Ответ. х = -8.
4. 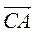 (-2; 0),
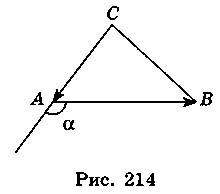
(-2; 0), 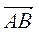 (1; 1) (рис. 214).
(1; 1) (рис. 214). 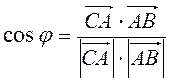 =
= 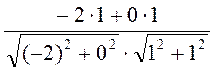 =
= 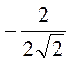 =
= 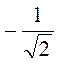 =
= 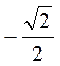 , отсюда α = 135°. Ответ. 135°.
, отсюда α = 135°. Ответ. 135°.
Вариант 2
1. 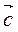 (2 ∙ 1 - 3; 2 ∙ 1 - 1) =
(2 ∙ 1 - 3; 2 ∙ 1 - 1) = 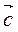 (-1; 1). Ответ.
(-1; 1). Ответ. 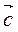 (-1; 1).
(-1; 1).
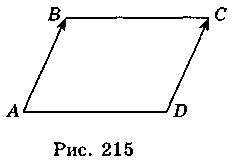
2. Пусть С(х; у), тогда 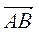 (1; 2),
(1; 2), 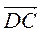 (х - 3; у + 3) (рис. 215). Поскольку
(х - 3; у + 3) (рис. 215). Поскольку 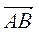 =
=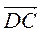 , то
, то 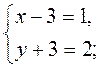
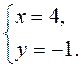 Следовательно, С(4; -1). Ответ. С(4; -1).
Следовательно, С(4; -1). Ответ. С(4; -1).
3. Данные векторы перпендикулярны, если 4 ∙ х + 2 ∙ (-4) = 0, тогда 4х - 8 = 0; 4х = 8; х = 2. Ответ. 2.
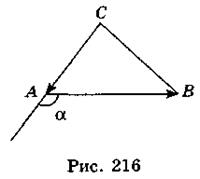
4. 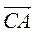 (-2; 0),
(-2; 0), 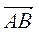 (1; 1), тогда (рис. 216)
(1; 1), тогда (рис. 216) 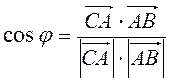 =
= 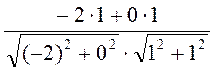 =
= 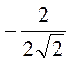 =
= 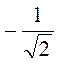 =
= 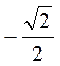 , отсюда α = 135°. Ответ. 135°.
, отсюда α = 135°. Ответ. 135°.
Вариант 3
1. 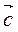 (-1 - 3 ∙ 1; 2 - 3 ∙ (-2)) =
(-1 - 3 ∙ 1; 2 - 3 ∙ (-2)) = 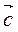 (-4; 8). Ответ.
(-4; 8). Ответ. 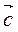 (-4; 8).
(-4; 8).
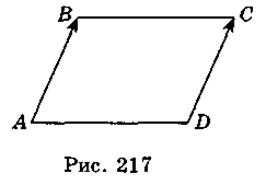
2. Пусть С(х; у), тогда 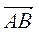 (3;2),
(3;2), 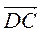 (x + 2; y - 1) (рис. 217). Поскольку
(x + 2; y - 1) (рис. 217). Поскольку 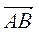 =
= 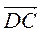 , то
, то 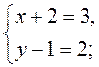
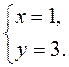 Следовательно, С(1; 3). Ответ. С(1; 3).
Следовательно, С(1; 3). Ответ. С(1; 3).
3. Данные векторы перпендикулярны, если 2 ∙ (-6) + 5 ∙ в = 0, отсюда -12 + 5у = 0; 5у = 12; в = 2,4. Ответ. 2,4.
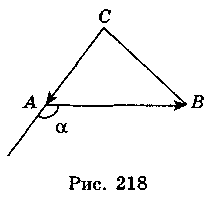
4. 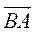 (-1; -1),
(-1; -1), 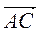 (2; 0) (рис. 218), тогда
(2; 0) (рис. 218), тогда
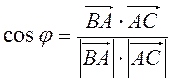 =
=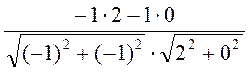 =
= 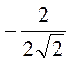 =
= 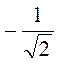 =
= 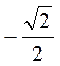 , отсюда α = 135°. Ответ. 135°.
, отсюда α = 135°. Ответ. 135°.
Вариант 4
1. 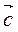 (3 ∙ (-1) - 1; 3 ∙ 2 - (-2)) =
(3 ∙ (-1) - 1; 3 ∙ 2 - (-2)) = 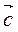 (-4; 8). Ответ.
(-4; 8). Ответ. 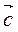 (-4; 8).
(-4; 8).
2. Пусть А(х; у), тогда 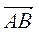 (1 - х; 3 - в),
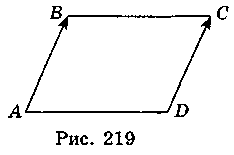
(1 - х; 3 - в), 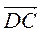 (1; 2) (рис. 219). Поскольку
(1; 2) (рис. 219). Поскольку 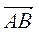 =
= 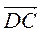 , то
, то 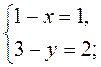
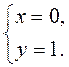 Следовательно, А(0; 1). Ответ. А(0; 1).
Следовательно, А(0; 1). Ответ. А(0; 1).
3. Векторы коллинеарны, если 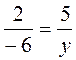 , отсюда 2у = -30; у = -15. Ответ. -15.
, отсюда 2у = -30; у = -15. Ответ. -15.
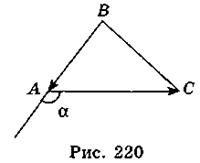
4. 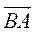 (-1; -1),
(-1; -1), 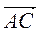 (2; 0) (рис. 220), тогда
(2; 0) (рис. 220), тогда
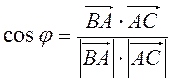 =
=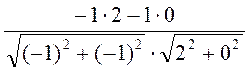 =
= 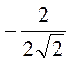 =
= 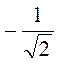 =
= 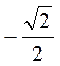 , отсюда α = 135°. Ответ. 135°.
, отсюда α = 135°. Ответ. 135°.
Тематическое оценивание № 5 можно провести в виде теста.
Тестовая работа
Вариант 1
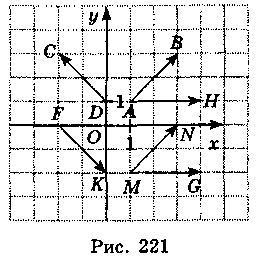
Пользуясь рис. 221, выполните задания 1-6.
I уровень
- 1. Найдите координаты вектора
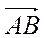 .
.
А. (1; 1); Б. (-2; 2); В. (2; 2); Г. (2; -2).
- 2. Укажите координаты вектора -
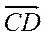 .
.
А. (-2; 2); Б. (2; -2); В. (2; 2); Г. (-2; -2).
- 3. Укажите вектор, равный вектору
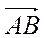 .
.
A. 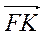 ; Бы.
; Бы. 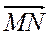 ; В.
; В. 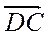 ; Г.
; Г. 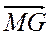 .
.
II уровень
- 4. Укажите координаты вектора
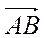 +
+ 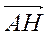 .
.
А. (2; 5); Б. (1; 2); В. (5; 2); Г. (1; -2).
- 5. Укажите координаты вектора
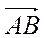 -
- 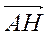 .
.
А. (1; 2); Б. (-1; 2); В. (1; -2); Г. (-1; -2).
- 6. Найдите
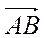 ∙
∙ 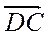 .
.
А. 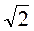 ; Бы. 2; В. 0; Г. 1.
; Бы. 2; В. 0; Г. 1.
III уровень
- 7. При каком значении векторы
 (1; -1) и
(1; -1) и  (n; 1) коллинеарны?
(n; 1) коллинеарны?
А. Ни при каких n; Б. n = -1;
В. n = 1; Г. n = ±1.
- 8. При каком значении п векторы
 (1; 1) и
(1; 1) и  (n; 1) перпендикулярны?
(n; 1) перпендикулярны?
А. n = 1; Б. n = -1;
В. n = ±1; Г. ни при каких n.
- 9. Найдите координаты вершины D параллелограмма ABCD, если А(0; 2), В(1; 0), С(2; 0).
А. D(1; 2); Б. D(2; 2); В. D(1; -2); Г. D(2; 1).
IV уровень
- 10. Даны точки A(2; 1), B(3; 2), C(3; 1). Найдите внутренний угол С треугольника ABC.
А. 30°; Б. 45°; В. 60°; Г. 90°.
- 11. Найдите площадь четырехугольника ABCD, если А(0; 1), В(1; 3), С(2; 1), D(1; -1).
А. 2; Б. 4; В. 6; Г. 8.
- 12. Найдите угол А треугольника ABC, если А(0; 1), В(
 ; 2), С(
; 2), С( ; 1).
; 1).
А. 30°; Б. 45°; В. 60°; Г. 90°.
Вариант 2
Пользуясь рис. 222, выполните задания 1-6.
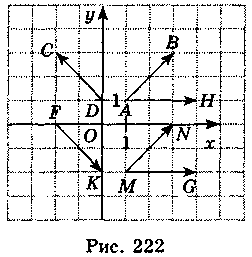
I уровень
- 1. Найдите координаты вектора
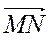 .
.
А. (1; 1); Б. (-2; 2); В. (2; 2); Г. (2; -2).
- 2. 2. Укажите координаты вектора -
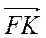 .
.
А. (-2; 2); Б. (2; -2); В. (2; 2); Г. (-2; -2).
- 3. Укажите вектор, равный вектору
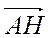 .
.
А. 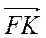 ; Бы.
; Бы. 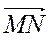 ; В.
; В. 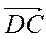 ; Г.
; Г. 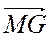 .
.
II уровень
- 4. Укажите координаты вектора
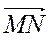 +
+ 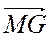 .
.
А. (2; 5); Б. (1; 2); В. (5; 2); Г. (1; -2).
- 5. Укажите координаты вектора
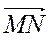 -
- 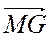 .
.
А. (1; 2); Б. (-1; 2); В. (1; -2); Г. (-1; -2).
- 6. Найдите
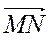 ∙
∙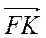 .
.
А. 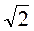 ; Бы. 2; В. 0; Г. 1.
; Бы. 2; В. 0; Г. 1.
III уровень
- 7. При каком значении п векторы
 (-1; 1) и
(-1; 1) и  (п; -1) коллинеарны?
(п; -1) коллинеарны?
А. n = 1; Б. n = -1; В. n = ±1; Г. ни при каких n.
- 8. При каком значении п векторы
 (1; -1) и
(1; -1) и  (п; 1) перпендикулярны?
(п; 1) перпендикулярны?
А. Ни при каких n; Б. n = -1; В. n = 1; Г. n = ±1.
- 9. Найдите координаты вершины А параллелограмма ABCD, если В(1; 0), C(1; 1), D(-1; 0).
А. А(2; 1); Б. А(-1; -1); В. А(0; 1); Г. А(0; -1).
IV уровень
- 10. Даны точки A(1; 1), В(2; 1), С(2; 2). Найдите внутренний угол А треугольника ABC.
А. 30°; Б. 45°; В. 60°; Г. 90°.
- 11. Найдите площадь четырехугольника ABCD, если A(1; 1), В(2; 3), С(3; 1), D(2; -1).
А. 2; Б. 4; В. 6; Г. 8.
- 12. Найдите угол В треугольника ABC, если А(0; -1), В(
 ; 0), С(
; 0), С( ; -1).
; -1).
А. 30°; Б. 45°; В. 60°; Г. 90°.
Ответы к тестовым заданиям
Уровень |
Номер задания |
Вариант 1 |
Вариант 2 |
И |
1 |
В |
В |
2 |
А |
А |
3 |
Б |
Г |
II |
4 |
В |
В |
5 |
Б |
Б |
6 |
В |
В |
III |
7 |
Б |
А |
8 |
Б |
В |
9 |
А |
Б |
IV |
10 |
Г |
Б |
11 |
Б |
Б |
12 |
А |
В |
II. Домашнее задание
Если в классе выполнялась тематическая контрольная работа № 5, то дома можно предложить тест, и наоборот.
III. Подведение итогов урока
Выяснить, какие задания вызвали затруднения у учащихся, и ответить на вопросы учеников.