Урок № 52

Тема. Теорема Виета

Цель: закрепить знания учащихся относительно содержания теоремы Виета для сводного квадратного уравнения и использовать их для формулировки и доказательства теоремы Виета для квадратного уравнения общего вида; совершенствовать умение воспроизводить изученные утверждение, использовать их для решения задач, предусмотренных программой по математике.

Тип урока: применение и совершенствование умений.

Наглядность и оборудование: опорный конспект «Теорема Виета».

Ход урока

I. Организационный этап

II. Проверка домашнего задания

Математический диктант

Закончите предложения:

1) сумма х1 + х2 корней уравнения х2 - bх + т = 0 равна...;

2) произведение в1 · у2 корней уравнения у2 + ау + b = 0 равна...;

3) сумма и произведение корней уравнения х2 - 5х + 6 = 0 соответственно равны...;

4) квадратное уравнение с целыми коэффициентами, сумма корней которого - 0,5, а произведение корней которого равен 2, имеет вид...

III. Формулировка цели и задач урока

После проведенной работы по проверке усвоения материала предыдущего урока (проверка качества выполнения математического диктанта), что предполагает неоднократное воспроизведение теоремы Виета для квадратного уравнения общего вида, формулируем проблему: существует ли соответствующим образом записан связь между корнями и коэффициентами квадратного уравнения общего вида, а также возможно ли применение выявленных закономерностей в ситуациях, подобных тем, что были рассмотрены на предыдущем уроке.

IV. Актуализация опорных знаний умений .та

@ С целью успешного восприятия учащимися учебного материала урока следует активизировать знания и умения учащихся: определение квадратного уравнения, виды квадратных уравнений; решение квадратных уравнений различных видов изученными способами; формулировка теоремы Виета и обратной к ней теоремы для сводного квадратного уравнения; выполнение арифметических действий с действительными числами.

Выполнение устных упражнений

1. Проверьте, являются ли числа х1 и х2 корни квадратного уравнения:

а) х2 - 9х + 14 = 0; х1 = 2; х2 = 7;

б) х2 + 2х - 3 = 0; х1 = -1; х2 = 3;

в) х2 + 3,5 х - 2 = 0; х1 = 0,5; х2 = - 4;

г) 3х2 - 7х + 2 = 0; х1 = 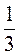; х2 = 2.

2. Решите уравнение:

а) 2х2 - 7 = 1;

б) х(х + 2,5) = 0;

в) х2 - 3х = 0;

г) х2 + 10х + 25 = 0;

д) 2х2 + 4 = 0;

есть) х2 - 6 = 0;

ж) х2 - х - 2 = 0;

с) х2 - х + 5 = 0.

V. Применение знаний

План изучения нового материала

1. Теорема Виета для квадратного уравнения общего вида.

2. Теорема, обратная теореме Виета для квадратного уравнения общего вида.

3. Примеры задач на применение изученных теорем.

@ Теорема Виета для квадратного уравнения общего вида и обратная к ней теорема приходятся довольно легко через теорему Виета для сводного квадратного уравнения.

Поэтому при высокой интеллектуальной активности учащихся можно предложить им изучения этой части нового материала самостоятельно (или за учебником, или сформулировать утверждение вместе с учениками, а затем предложить им выполнить доведение самостоятельно).

Относительно примеров применения изученных теорем (обычно в этом разделе рассматриваются только задачи на нахождение неизвестного корня и одного из коэффициентов по известным вторым корнем и двумя известными коэффициентами квадратного уравнения общего вида), то здесь автор предлагает ознакомить учащихся с некоторыми приемами решения квадратных уравнений, основанные на применении теоремы, обратной теореме Виета (например, для уравнений вида ах2 + bx + c = 0, где а + с = b, х1 = -1, х2 = ).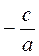

VI. Отработка умений

Выполнение устных упражнений

1. Найдите сумму и произведение корней уравнения:

а) 2х2 - 5х - 2 = 0;

б) 3х2 - 2х - 1 = 0;

в) 5х2 + 4х - 1 = 0;

г) 7х2 - 8х + 1 = 0.

2. Среди уравнений ах2 + bx + c = 0 выберите такие, в которых: а) а + с = b; б) а + с = -b.

х2 - 2х + 1 = 0;

3х2 - 2х - 1 = 0;

5х2 + 4х - 1 = 0;

122х2 + 33x - 89 = 0.

3. Найдите корни уравнения:

а) 3х2 - 2х - 1 = 0;

б) 3х2 + 2х - 1 = 0;

в) 199х2 - 100х - 99 = 0;

г) 199х2 + 100х - 99 = 0.

Выполнение письменных упражнений

Для реализации дидактической цели на этом уроке следует решить задачи следующего содержания:

1. Нахождение корней квадратного уравнения по теореме, обратной теореме Виета.

1) Найдите корни уравнения по теореме, обратной теореме Виета:

а) х2 - 3x + 2 = 0;

б) х2 - 5х + 6 = 0;

в) х2 + 7x + 12 = 0;

г) х2 + 3x + 2 = 0;

д) x2 - 5x + 4 = 0;

есть) х2 - 8x - 9 = 0;

ж) х2 + 4х + 3 = 0;

с) х2 - 2х - 3 = 0;

ы) х2 + 2х - 15 = 0.

2) Найдите подбором корни уравнения:

а) х2 - 9х + 20 = 0;

б) х2 + 11x - 12 = 0;

в) х2 + х - 56 = 0;

г) x2 - 19x + 88 = 0.

3) Решите уравнение:

а) 4х2 + 7x + 3 = 0;

б) х2 + х - 56 = 0;

в) х2 - х - 56 = 0;

г) 5х2 - 18x + 16 = 0;

д) 8х2 + х - 75 = 0;

есть) 3х2 - 11х - 14 = 0;

ж) 3х2 + 11х - 34 = 0;

с) х2 - х - 1 = 0.

2. Нахождение коэффициентов сводного квадратного уравнения и квадратного уравнения общего вида по его известными корнями.

1) Числа х1 и х2 - корни сводного квадратного уравнения. Запишите это уравнение, если:

а) х1 + х2 = 4, х1 · х2 = 3;

б) х1 + х2 = -7, х1 · х2 = 10.

2) Запишите сведено квадратное уравнение, которое имеет корни: а) 1 и 3; б) -4 и 1,5; в) -4 и -5; г) 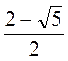и .

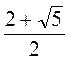3) При каком значении а один из корней уравнения ах2 - 3х - 5 = 0 равен 1?

3. Нахождение неизвестного корня и неизвестного коэффициента квадратного (сводного и общего вида) уравнения, если известен второй корень и два другие коэффициенты.

1) Число - 9 является корнем уравнения х2 + 10x + q = 0. Найдите другой корень уравнения и коэффициент q.

2) Какими могут быть целые корни уравнения х2 + px + q = 0, если: a) q = 7; б) q = -5; в) q = 9; г) q = -8?

3) Один из корней уравнения х2 - 13х + q = 0 равна 12,5. Найдите второй корень и коэффициент q.

4. Логические упражнения и задачи повышенного уровня сложности для учащихся, имеющих достаточный и высокий уровни знаний.

1) Уравнение х2 + рх + 8 =0 имеет положительные корни, один из которых в 4 раза больше другого. Найдите корни уравнения и коэффициент р.

2) Докажите, что уравнение 12х2 + 70х + a2 + 1 = 0 при любых значениях а не имеет положительных корней.

3) Найдите пропущенный выражение:

5. На повторение: решить квадратные уравнения, определив предварительно их вид.

@ Упражнения, вынесенные на урок, имеют целью способствовать закреплению содержания теоремы Виета и обратной к ней теоремы, отработка навыков использования изученной теории в стандартных ситуациях.

VII. Итоги урока

В каком случае правильно записаны соотношения для корней?

а) х2 + 3х + 2 = 0, х1 + х2 = 3, х1 · х2 = 2;

б) 3х2 - 2х - 1 = 0, х1 + х2 = 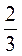, х1 · х2 = 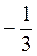, х1 = 1;

в) 3х2 + 2х - 5 = 0, х1 + х2 = 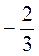, х1 · х2 = 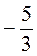, х1 = - 1.

VIII. Домашнее задание

1. Изучить содержание теоремы Виета и обратной к ней теоремы для квадратного уравнения общего вида.

2. Решить задачи на применение изученной теории (найти корни квадратного уравнения по теореме, обратной теореме Виета; найти неизвестный корень и неизвестный коэффициент квадратного (сводного и общего вида) уравнения, если известен второй корень и два другие коэффициенты).

3. На повторение: задачи, предусматривающие решения квадратных уравнений (полных и неполных с применением изученных в теме 5 способам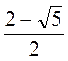и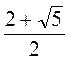).