В реальных условиях происходит нестационарная диффузия. По нестационарных условиях, когда имеем смесь с неравномерным распределением каких-либо компоненты, во время диффузии концентрации выравниваются. Поэтому при нестационарной диффузии градиент концентрации и сами концентрации компонент меняются.

Пусть два сосуда с объемами V₁ и V₂ соединены между собой трубкой длиной l с плоскостью сечения s (рис. 5.3) и наполненные смесью газов разного состава, но при одинаковых давлений и температур, а концентрации заданной компоненты в обоих сосудах равны соответственно n₁ и n₂, a n₁ > n₂.

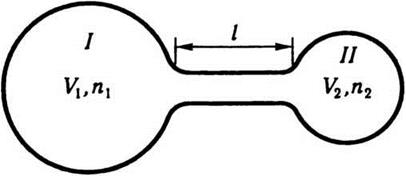
Рис. 5.3

Вследствие диффузии концентрации в обоих сосудах вирівнюватимуться, то есть разница концентраций Δn = n₁ - n₂ со временем будет уменьшаться.

Определим закон, по которому уменьшается разница концентраций. Из закона Фика следует, что диффузионный поток

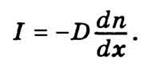
Предположим, что концентрация заданной компоненты мала. Тогда можно записать, что

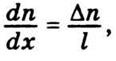
а уравнение (5.11) приобретет такой вид:

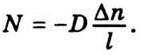
В процессе диффузии молекулы диффундирующей компоненты будут переходить из сосуда И в сосуд II. По бесконечно малый промежуток времени dt количество молекул, которые продифундують в сосуд II, равна

Поскольку молекулы переходят из первой посудины в другую, их плотность в сосуде И уменьшится на некоторую величину dn', а в сосуде II в соответствии увеличится на величину dn’. Можно еще записать так:

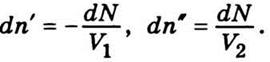
Поэтому концентрации n₁ и n₂ молекул в сосудах И и II за время dt станут другими:

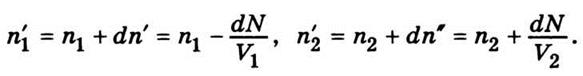
Определим разность концентраций через время dt:

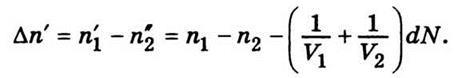
Подставим сюда значение dN из (5.13), а разницу n₁ - n₂ обозначим через Δn, после чего получим

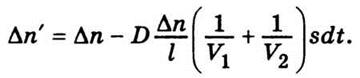
Отсюда следует, что изменение разницы концентраций за время dt равна

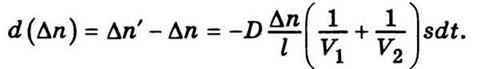
Величину 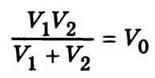называют сводным объемом (при V₁ = V₂ = V сводный объем V₀ = V/2 ).

Следовательно,

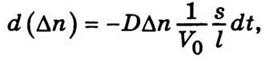
или

После интегрирования (5.14) получим

где А - постоянная интегрирования. Отсюда

Стала А определяется из условия, когда известна начальная разность концентраций Δn₀, то есть разница концентраций в момент времени t = 0. Подставим эти значения времени в (5.16) и получим, что А = Δn₀, тогда

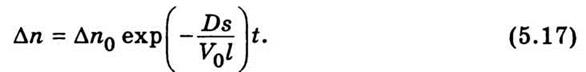
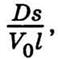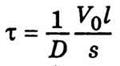Это равенство дает ответ на поставлен вопрос о закон уменьшения разности концентраций со временем. Разница концентраций со временем уменьшается по экспоненциальному закону и тем быстрее, чем больше значение величины которая для этого примера является постоянной величиной. Величина, обратная этой постоянной, имеет размерность времени. Суть постоянной τ заключается в том, что она равна промежутка времени, который нужен для того, чтобы концентрация диффундирующей компоненты уменьшилась в е раз. Величину τ называют постоянной времени процесса.

Уравнение (5.17) можно записать так:

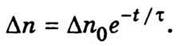
Следовательно, чем меньше постоянная времени, тем быстрее происходит процесс выравнивания.

Диффузия в газах при атмосферном давления - процесс медленный.

Например, для смеси азота и кислорода разница концентраций уменьшится втрое только за 5 ч.