|
III. Формулировка цели и задач урока Учитель сообщает ученикам, что изучение понятие площади многоугольника, ее свойств и формул для вычисления площадей изученных видов четырехугольников, треугольников, кроме сугубо практического направления, имеет еще и методологическое значение, то есть дает на вооружение ученикам еще один метод решения задач (и не только задач, в которых речь идет о вычислении площадей). Итак, цель урока - изучение схемы действий, предусмотренной содержанием понятия «метод площадей», а также формирование умений применять эту схему при решении задач.
IV. Актуализация опорных знаний Поскольку материал урока основан на применении изученных ранее формул площадей в новой ситуации согласно схеме, описанной в комментарии к методу площадей, то учащимся следует повторить формулы площадей, их последствия и способы применения в стандартных ситуациях.
Выполнение письменных упражнений по готовым рисункам
V. Усвоение знаний @ Содержание учебного материала урока является полезным дополнением, сделанным авторами нового учебника до традиционного содержания материала, который изучался в теме «Плоти», и является обобщением тех способов действий, которые, возможно, выполняли ученики, изучая эту тему в предыдущие годы. К изучению на уроке предлагается рассмотрение способов решения некоторых задач, связанных с применением вычисления площадей по изученным в классе формулами. Изучение материала на уроке проводится по учебнику (как вариант - предложить сначала решить задачу самостоятельно, а после исполнения обратиться к учебнику), причем необходимо не просто ознакомиться с содержанием решения, но и провести работу по его осознание (эту работу можно провести в форме беседы) Результат этой работы должен иметь вид определенной схемы действий, что содержит признаки, по которым можно определить среди других задачу, в которой возможно применить метод площадей, а также примерное описание действий во время решения задач этим методом.
VI. Формирование первичных умений Выполнение письменных упражнений 1. Две стороны треугольника равны 12 см и 18 см. Найдите высоту, проведенную к меньшей из них, если высота, проведенная к большей стороне, равна 4 см. 2. Пользуясь методом площадей, докажите, что в рівнобедреному треугольнике высоты, проведенные к боковым сторонам, равны. 3. Периметр параллелограмма равен 56 см. Найдите стороны параллелограмма, если его высоты равны 6 см и 8 см. 4. Диагонали ромба равны 30 см и 40 см. Пользуясь методом площадей, найдите высоту ромба. 5. Докажите методом площадей, что параллелограмм с равными высотами является ромбом. 6*. Прямая, параллельная стороне треугольника, делит его на две равновеликие части. В каком отношении эта прямая делит две другие стороны треугольника? 7. Докажите, что стороны треугольника обратно пропорциональны его высотам:
VII. Домашнее задание Повторить теоретический материал по теме «Площади многоугольников». Выполнить тестовое задание. 1. Назовите формулу площади трапеции с основаниями а и b и высотой А. а) 2. Назовите формулу площади ромба с диагоналями d1 и d2. 3. Площадь треугольника ABC равна S. Найдите площадь треугольника, который отсекает от треугольника ABC средняя линия. a) 4. По данным рисунка найдите площадь трапеции A BCD , если ее средняя линия равна 10. а) 120; б) 300; в) 150; г) 136.
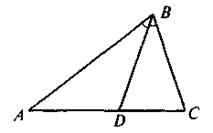
5. Отрезок BD - биссектриса треугольника ABC (рисунок). Площади треугольников BDC и ABC относятся как 4 : 9. Найдите отношение АВ.ВС. а) 5: 2; б) 4 : 5; в) 3 : 2; г) 5 : 4.
Решить задачи. 1. Высоты параллелограмма равны 6 см и 4 см, а меньшая сторона - 8 см. Найдите периметр параллелограмма. 2. Докажите методом площадей, то треугольник с равными высотами является равносторонним. 3. Докажите методом площадей метрическое соотношение в прямоугольном треугольнике 4. Сумма расстояний от точки основания равнобедренного треугольника до его боковых сторон не зависит от выбора точки. Докажите.
|
|
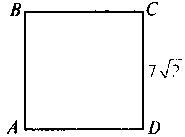
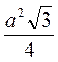
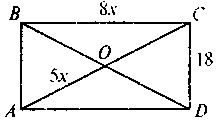
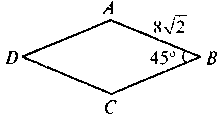
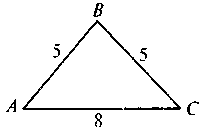
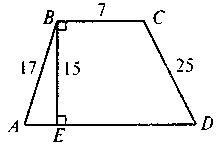
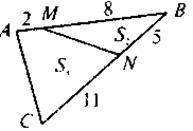
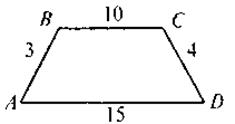
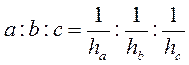 .
. ; б)
; б) 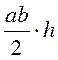 ; в)
; в) 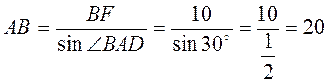 .
.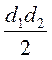 ; г)
; г) 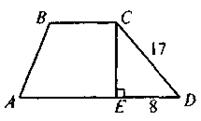
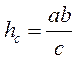 .
.